
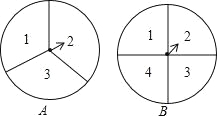
【题目】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】用配方法解方程x2﹣2x﹣6=0时,原方程应变形为( )
A.(x+1)2=7
B.(x﹣1)2=7
C.(x+2)2=10
D.(x﹣2)2=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.同一平面内,过一点有且只有一条直线与已知直线平行
C.与同一条直线垂直的两条直线也垂直
D.同一平面内,过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
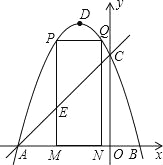
【题目】如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A,B,C三点的坐标.
(2)点M为线段AB上一点(点M不与点A,B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积.
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连结DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长. ![]()
请补全以下解答过程.
解:∵D,B,E三点依次在线段AC上,
∴DE=+BE.
∵AD=BE,
∴DE=DB+=AB.
∵DE=4,
∴AB=4.
∵ ,
∴AC=2AB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 三角形的角平分线都在三角形内部 B. 三角形的三条高都在三角形内部
C. 三角形的三条中线都在三角形内部 D. 三角形的三条角平分线相交于一点
查看答案和解析>>
科目:初中数学 来源: 题型:
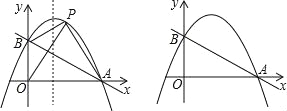
【题目】如图,直线y=﹣![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com