
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.

(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如下图表所示:
销售量n(株) |
|
销售单价 m(元/株) | 当1≤x≤20时,m=________ |
当21≤x≤30时, |
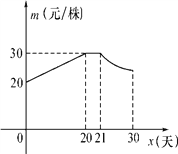
(1)①请将表中当1≤x≤20时,m与x间关系式补充完整;
②计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里每天所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”。试问:基地负责人这次为“精准扶贫”捐赠多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
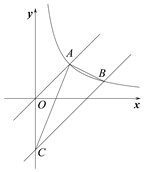
【题目】如图,直线OA与反比例函数![]() (
(![]() )的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数
)的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数![]() (
(![]() )的图像交于点B(6,m),与y轴交于点C.
)的图像交于点B(6,m),与y轴交于点C.
(1)求直线BC的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
(1)求证:DE∥AB;
(2)当x=1时 ,求点E到AB的距离;
(3) 将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.
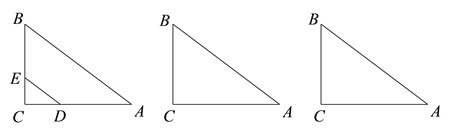
图1 备用图1 备用图2
查看答案和解析>>
科目:初中数学 来源: 题型:
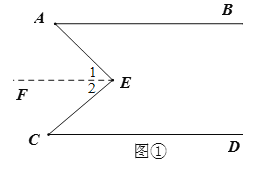
【题目】(1)(感知)如图①,![]() ,点
,点![]() 在直线
在直线![]() 与
与![]() 之间,连接
之间,连接![]() 、
、![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
.下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
证明:如图①过点![]() 作
作![]() .
.
![]() ( ),
( ),
![]() (已知),EF
(已知),EF![]() (辅助线作法),
(辅助线作法),
![]() ( ),
( ),
![]() ( ),
( ),
![]() ,
,
![]() ( ).
( ).
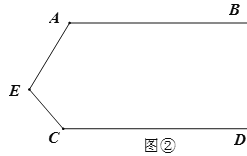
(2)(探究)当点![]() 在如图②的位置时,其他条件不变,试说明
在如图②的位置时,其他条件不变,试说明![]() .
.
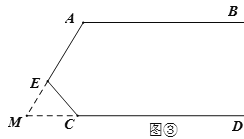
(3)(应用)如图③,延长线段![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 的度数为 .(请直接写出答案)
的度数为 .(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
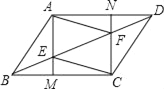
【题目】如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com