
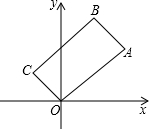
 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.分析 (1)根据d(P)=|x|+|y|,即可求得点A的坐标距离d(A);
(2)①先过点A作AE⊥x轴于E,作CF⊥x轴于F,则∠CFO=∠OEA=90°,再设A(a,b),C(m,n),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,通过判定△CFO∽△OEA,可得$\frac{CF+OF}{OE+AE}$=$\frac{1}{2}$,即$\frac{|n|+|m|}{|a|+|b|}$=$\frac{1}{2}$,据此可得d(A)=d(C)×2;
②先过点B作BG⊥CF,交CF的延长线于G,交y轴于H,则GF=OH,GH=OF,∠G=∠AEO=90°,再通过判定△BCG≌△OAE(AAS),得出OE=BG,AE=CG,BG=OE,然后由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,最后根据d(A)+d(C)=d(B)+2,即可得出OE+AE+OF+CF=BH+GF+2,将BH=BG-GH=OE-OF,GF=CG+CF=AE+CF代入后,可得OE+AE+OF+CF=(OE-OF)+(AE+CF)+2,求得OF=1,再根据勾股定理以及相似三角形的对应边成比例,即可得出FG=CG+CF=2+$\sqrt{3}$=OH,BH=BG-OF=2$\sqrt{3}$-1,进而得到点B的坐标.
解答 解:(1)∵点A(3,-4),
∴点A的坐标距离d(A)=|3|+|-4|=3+4=7;
(2)①证明:如图,过点A作AE⊥x轴于E,作CF⊥x轴于F,则∠CFO=∠OEA=90°,
设A(a,b),C(m,n),则|a|=OE,|b|=AE,|m|=OF,|n|=CF,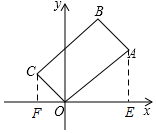
∵矩形ABCO中,∠AOC=90°,
∴∠AOE+∠COF=90°,
又∵∠AOE+∠EAO=90°,
∴∠COF=∠OAE,
∴△CFO∽△OEA,
∴$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=$\frac{1}{2}$,
∴$\frac{CF+OF}{OE+AE}$=$\frac{1}{2}$,即$\frac{|n|+|m|}{|a|+|b|}$=$\frac{1}{2}$,
即|a|+|b|=(|m|+|n|)×2,
∴d(A)=d(C)×2;
②如图所示,过点B作BG⊥CF,交CF的延长线于G,交y轴于H,则GF=OH,GH=OF,∠G=∠AEO=90°,
∵∠BCO=90°=∠CFO,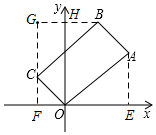
∴∠BCG+∠FCO=∠COF+∠FCO=90°,
∴∠BCG=∠COF,
∵∠COF=∠OAE,
∴∠BCG=∠OAE,
∵四边形ABCO是矩形,
∴CB=AO,
在△BCG和△OAE中,
$\left\{\begin{array}{l}{∠BCG=∠OAE}\\{∠G=∠AEO}\\{CB=AO}\end{array}\right.$,
∴△BCG≌△OAE(AAS),
∴OE=BG,AE=CG,BG=OE,
由图可得,d(A)=OE+AE,d(C)=OF+CF,d(B)=BH+OH=BH+GF,
∵d(A)+d(C)=d(B)+2,
∴OE+AE+OF+CF=BH+GF+2,
又∵BH=BG-GH=OE-OF,GF=CG+CF=AE+CF,
∴OE+AE+OF+CF=(OE-OF)+(AE+CF)+2,
∴即OF=2-OF,
∴OF=1,
∵Rt△COF中,CO=2,
∴CF=$\sqrt{3}$,
又∵$\frac{OC}{AO}$=$\frac{CF}{OE}$=$\frac{OF}{AE}$=$\frac{1}{2}$,
∴$\frac{\sqrt{3}}{OE}$=$\frac{1}{AE}$=$\frac{1}{2}$,即OE=2$\sqrt{3}$,AE=2,
∴BG=2$\sqrt{3}$,CG=2,
∴FG=CG+CF=2+$\sqrt{3}$=OH,BH=BG-OF=2$\sqrt{3}$-1,
∴B(2$\sqrt{3}$-1,2+$\sqrt{3}$).
点评 本题属于四边形综合题,主要考查了矩形的性质,相似三角形的判定与性质以及坐标与图形的性质的综合应用,解题时注意:坐标平面内点到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
 已知:如图所示.
已知:如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
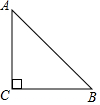 如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
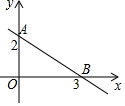 如图,直线AB对应的函数表达式是( )
如图,直线AB对应的函数表达式是( )| A. | y=-$\frac{3}{2}$x+2 | B. | y=$\frac{3}{2}$x+3 | C. | y=-$\frac{2}{3}$x+2 | D. | y=$\frac{2}{3}$x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com