
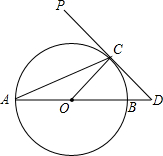
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.分析 (1)先证明∠COD=2∠A,由∠D=2∠A,得∠D=∠COD,再根据切线的性质即可解决问题.
(2)根据△OCD是等腰直角三角形即可求出CO、OD,由此即可解决问题.
解答  解:(1)∵PD切⊙O于点C,
解:(1)∵PD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∵OA=OC,
∴∠A=∠OCA,∠COD=2∠A,
∵∠D=2∠A,
∠D=∠COD=45°,
(2)由(1)可知,∠D=∠COD,
∴CD=CO=AO=$\sqrt{2}$,∵∠OCD=90°,
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=$\sqrt{2+2}$=2,
∴AD=AO+OD=$\sqrt{2}$+2.
点评 本题考查切线的性质、等腰直角三角形的性质、圆的有关性质、勾股定理等知识,解题的关键是熟练掌握这些知识的应用,属于基础题,中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 测量某天的最高气温是100℃ | |
| B. | 度量四边形的内角和,结果是360° | |
| C. | 掷一枚骰子,向上一面的数字是2 | |
| D. | 袋中装有5只黑球,从中摸出一个是黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
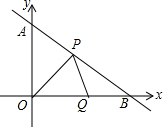 综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
综合与探究:如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com