
【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= . 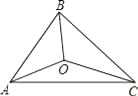
【答案】4:5:6
【解析】首先过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,由OA,OB,OC是△ABC的三条角平分线,根据角平分线的性质,可得OD=OE=OF,又由△ABC的三边AB、BC、CA长分别为40、50、60,即可求得S△ABO:S△BCO:S△CAO的值.
过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
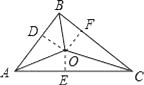
∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=( ![]() ABOD):(
ABOD):( ![]() BCOF):(
BCOF):( ![]() ACOE)=AB:BC:AC=40:50:60=4:5:6.
ACOE)=AB:BC:AC=40:50:60=4:5:6.
根据角平分线的性质可知,角平分线上的点到角两边的距离相等;求出S△ABO:S△BCO:S△CAO的值.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
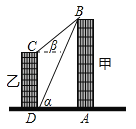
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽同学要画∠AOB的平分线,却没有量角器和圆规,于是她用三角尺按下面方法画角平分线: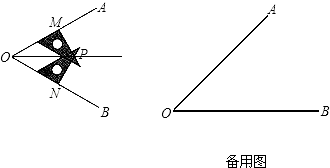
①在∠AOB的两边上,分别取OM=ON;
②分别过点M、N作OA、OB的垂线,交点为P;
③画射线OP,则OP为∠AOB的平分线.
(1)请问:小丽的画法正确吗?试证明你的结论;
(2)如果你现在只有刻度尺,能否画一个角的角平分线?请你在备用图中试一试.(不需要写作法,但是要让读者看懂,你可以在图中标明数据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人由相距60km的两地同时出发相向而行,甲步行每小时走5km,乙骑自行车,3h后相遇,则乙的速度为( )
A. 5 km/hB. 10 km/hC. 15 km/hD. 20 km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
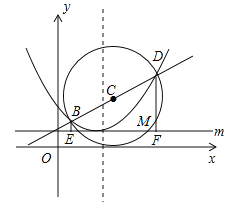
【题目】如图,已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线![]() 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com