
【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]()
![]() ,⊙M是△ABC的外接圆,M为圆心.
,⊙M是△ABC的外接圆,M为圆心.
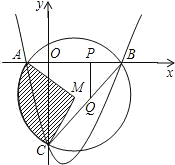
(1)求抛物线的解析式;
(2)求阴影部分的面积;
(3)在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=k,△CPQ的面积为S,求S关于k的函数关系式,并求出S的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
试题分析:
(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
试题解析:
解:(1)由抛物线经过![]() ,
,
设抛物线的解析式为:![]() ,
,
将![]() 代入上式中,得
代入上式中,得![]() .
.
∴![]() .
.
(2)∵![]() .
.
∴![]()
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.
(3)![]() ,
,![]() 轴;
轴;
∴![]() ,
,
∴![]() .
.
∴当![]() 时,
时,![]() .
.
考点: 二次函数综合题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
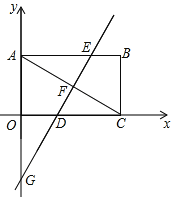
(1)求B、C两点的坐标;
(2)过点G(![]() )作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;
)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;
(3)在⑵的条件下,若点M在直线DE上,平面内是否存在点P,使以O、F、M、P为顶点的四边形是菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com