
【题目】如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB= ![]() πcm2;②
πcm2;② ![]() ;③∠ACB=20°;④∠ADB=140°.错误的有( )
;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个
B.1个
C.2个
D.3个
科目:初中数学 来源: 题型:
【题目】三角形ABC的三条内角平分线为AE、BF、CG,下面的说法中正确的个数有( )
①△ABC的内角平分线上的点到三边距离相等
②三角形的三条内角平分线交于一点
③三角形的内角平分线位于三角形的内部
④三角形的任一内角平分线将三角形分成面积相等的两部分.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△A'B'C'关于直线m对称.
(1)结合图形指出对称点;
(2)若连接AA',直线m与线段AA'有什么关系?
(3)BC与B'C'的交点,AB与A'B'的交点分别与直线m有怎样的关系?若延长AC与A'C',其交点与直线m有怎样的关系?你发现了什么规律?

查看答案和解析>>
科目:初中数学 来源: 题型:
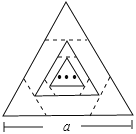
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y. 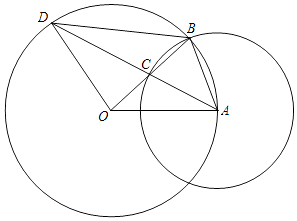
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
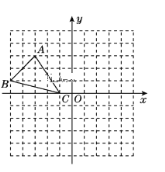
【题目】如图,已知网格上最小的正方形的边长为1,
(1)作△ABC关于![]() 轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于
轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于![]() 轴对称的两个点之间有什么关系?
轴对称的两个点之间有什么关系?
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com