
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
【答案】
(1)解:设y=kx+b,
把(22,36)与(24,32)代入得: ![]() ,
,
解得: ![]() ,
,
则y=﹣2x+80
(2)解:设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,
根据题意得:(x﹣20)y=150,
则(x﹣20)(﹣2x+80)=150,
整理得:x2﹣60x+875=0,
(x﹣25)(x﹣35)=0,
解得:x1=25,x2=35(不合题意舍去),
答:每本纪念册的销售单价是25元
(3)解:由题意可得:
w=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600
=﹣2(x﹣30)2+200,
此时当x=30时,w最大,
又∵售价不低于20元且不高于28元,
∴x<30时,y随x的增大而增大,即当x=28时,w最大=﹣2(28﹣30)2+200=192(元),
答:该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元
【解析】(1)设y=kx+b,根据题意,利用待定系数法确定出y与x的函数关系式即可;(2)根据题意结合销量×每本的利润=150,进而求出答案;(3)根据题意结合销量×每本的利润=w,进而利用二次函数增减性求出答案.


科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).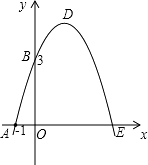
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为正整数),则有a+b
)2(其中a、b、m、n均为正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,
,
∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得:a= , b= .
)2,用含m、n的式子分别表示a、b,得:a= , b= .
(2)利用所探索的结论,找一组正整数a、b、m、n填空: + = ( + )2;(答案不唯一)
(3)若a+4![]() =(m+n
=(m+n![]() )2 ,且a、m、n均为正整数,求a的值.
)2 ,且a、m、n均为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+ ![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 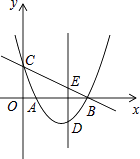
(1)求A、B的坐标;
(2)求直线BC的解析式;
(3)当线段DE的长度最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)用适当的方法解方程:
①(x﹣2)2=2x﹣4
②x2﹣2x﹣8=0.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣a+1),其中a是方程x2﹣x=6的根.
﹣a+1),其中a是方程x2﹣x=6的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长为( ) 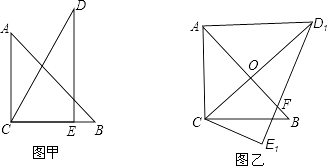
A.6 ![]()
B.10
C.8
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
计算:![]() .
.
解法一:原式=
![]()
解法二:原式=(-![]() )÷[(
)÷[(![]() )-(
)-(![]() )]=
)]=![]() ÷
÷![]() =-
=-![]() ×3=-
×3=-![]() .
.
解法三:原式的倒数为(![]() )÷(-
)÷(-![]() )=
)=![]() ×(-30)-
×(-30)-![]() ×(-30)+
×(-30)+![]() ×(-30)-
×(-30)-![]() ×(-30)=-20+3-5+12=-10,
×(-30)=-20+3-5+12=-10,
故原式=-![]() .
.
(1)上述解法得出的结果不同,肯定有错误的解法,你认为解法________是错误的,在正确的解法中,你认为解法________最简捷;
(2)利用(1)中你认为最简捷的解法计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com