
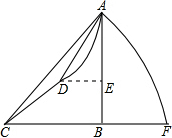
 小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$. 分析 作DF⊥CF,垂足为F,作DE⊥AB于点E,先判断出△ACD的形状,再由锐角三角函数的定义即可得出结论.
解答  解:作DF⊥CF,垂足为F,作DE⊥AB于点E.
解:作DF⊥CF,垂足为F,作DE⊥AB于点E.
∵∠ACB=45°,∠DCB=37°,
∴∠ACD=45°-37°=8°,∠CAB=45°,AB=BC..
∵∠ADE=53°,
∴∠DAE=90°-53°=37°,
∴∠CAD=45°-37°=8°,
∴AD=CD=200米.
在Rt△CDF中,CF=CD•cos37°=200×$\frac{4}{5}$=160(米).
在Rt△ADE中,DE=AD•cos53°=200×$\frac{3}{5}$=120(米).
∵DF⊥CF,EB⊥CF,DE⊥AB,
∴四边形DEBF是矩形,
∴DE=BF,
∴AB=BC=160+120=280(米).
答:山高AB是280米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示,有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法是( )
在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示,有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com