
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
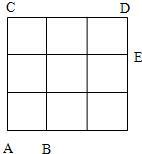 15、宋朝时,中国象棋就已经风靡于全国,中国象棋规定马步为:“
15、宋朝时,中国象棋就已经风靡于全国,中国象棋规定马步为:“ 、
、 ”形的对角线(即一次对角线为一步),现定义:在棋盘上从点A到点B,马走的最少步称为A与B的“马步距离”,记作dA->B.在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在dA->B,dA->C,dA->D,dA->E中小的是
”形的对角线(即一次对角线为一步),现定义:在棋盘上从点A到点B,马走的最少步称为A与B的“马步距离”,记作dA->B.在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在dA->B,dA->C,dA->D,dA->E中小的是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(0,21005) | B、(0,-21005) | C、(0,-21006) | D、(0,21006) |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
. |
| abc |
. |
| abc |
. |
| abc |

. |
| abc |
. |
| abc |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com