练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，函数y=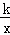的图象过点A（1，2）．

    （1）求该函数的解析式；

    （2）过点A分别向x轴和y轴作垂线，垂足为B和C，求四边形ABOC的面积；

    （3）求证：过此函数图象上任意一点分别向x轴和y轴作垂线，这两条垂线与两坐标轴所围成矩形的面积为定值．


    解：（1）∵函数y=的图象过点A（1，2），

    ∴将点A的坐标代入反比例函数解析式，

    得2=，解得：k=2，

    ∴反比例函数的解析式为y=；

    （2）∵点A是反比例函数上一点，

    ∴矩形ABOC的面积S=AC•AB=|xy|=|k|=2．

    （3）设图象上任一点的坐标（x，y），

    ∴过这点分别向x轴和y轴作垂线，矩形面积为|xy|=|k|=2，

    ∴矩形的面积为定值


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    甲,乙两人以相同路线前往距离单位10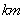的培训中心参加学习.图中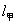, 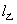分别表示甲,乙两人前往目的地所走的路程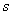随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8后遇到甲;④乙出发6分钟后追上甲.其中正确的有(               )

    A、4个

    B、3个

    C、2个

    D、1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组∶，并把解集在下面数轴上表示出来．

     

     

     

     

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小兰画了一个函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（　　）

    　

    A．

    无解

    B．

    x=1

    C．

    x=﹣4

    D．

    x=﹣1或x=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD、△BCE、△ABC的面积分别是S1、S2、S3，现有如下结论：

    ①S1：S2=AC2：BC2；

    ②连接AE，BD，则△BCD≌△ECA；

    ③若AC⊥BC，则S1•S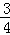2=S32．

    其中结论正确的序号是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    去年我市参加中考人数约17700人，这个数用科学记数法表示是（　　）

    　

    A．

    1.77×102

    B．

    1.77×104

    C．

    17.7×103

    D．

    1.77×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    顺次连接菱形各边的中点所形成的四边形是（　　）

    　

    A．

    等腰梯形

    B．

    矩形

    C．

    菱形

    D．

    正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


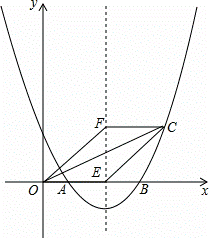
    如图，抛物线y=ax2+bx+2与x轴交于点A（1，0）和B（4，0）．

    （1）求抛物线的解析式；

    （2）若抛物线的对称轴交x轴于点E，点F是位于x轴上方对称轴上一点，FC∥x轴，与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标；

    （3）在（2）的条件下，抛物线的对称轴上是否存在点P，使△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是上的一个动点，连接AP，则AP的最小值是　　．

    查看答案和解析>>

    同步练习册答案