
分析 (1)先得出BH=$\frac{1}{2}$BD,再判断出△ABC≌△EBF,得出EF=AC,然后用勾股定理,借助图形中线段的关系推导即可得出结论;
(2)同(1)的方法构造出全等三角形,用(1)的方法即可得出结论;
(3)同(1)的方法即可.
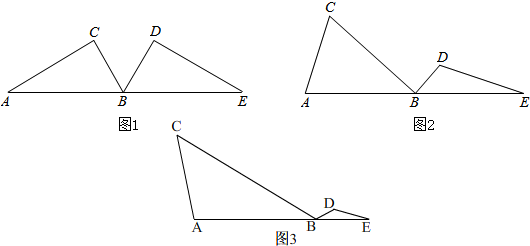
解答 解:(1)如图1,
过点D作DH⊥BC,
∴∠DHB=90°,
∵∠DBH=60°,
∴BH=BDcos∠DBH=BDcos60°=$\frac{1}{2}$BD;
延长CB至F,使BF=BC,
在△ABC和△EBF中,$\left\{\begin{array}{l}{BC=BF}\\{∠ABC=∠EBF}\\{AB=EB}\end{array}\right.$,
∴△ABC≌△EBF,
∴EF=AC,∠BEF=∠BAC,
∵∠CBD=∠CAB+∠DEB,
∴∠DEF=∠DEB+∠BEF=∠DEB+∠BAC=∠CBD=60°,
连接DF,
∵EF=AC,DE=AC,
∴DE=EF,
∴△DEF是等边三角形,
∴DF=DE=AC,
在Rt△BDH中,DH2=BD2-BH2,
在Rt△FDH中,DF2=FH2+DH2=(BF+BH)2+BD2-BH2=BF2+BH2+2BF•BH+BD2-BH2=BC2+BD2+2BC•$\frac{1}{2}$BD=BC2+BD2+BC•BH,
∴AC2=BC2+BD2+BC•BH,
故答案为:AC2=BC2+BD2+BC•BH;
(2)2AC2=BD2+BC2,
理由:如图2,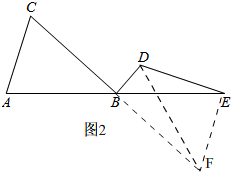
延长CB至F,使BF=BC,
在△ABC和△EBF中,$\left\{\begin{array}{l}{BC=BF}\\{∠ABC=∠EBF}\\{AB=EB}\end{array}\right.$,
∴△ABC≌△EBF,
∴EF=AC,∠BEF=∠BAC,
∵∠CBD=∠CAB+∠DEB,
∴∠DEF=∠DEB+∠BEF=∠DEB+∠BAC=∠CBD=90°,
连接DF,
∵EF=AC,DE=AC,
∴DE=EF,
∴△DEF是等腰直角三角形,
∴DF2=2DE2=2AC2,
∵∠DBC=90°,
∴∠DBF=90°,
在Rt△DBF中,DF2=BD2+BF2=BD2+BC2,
∴2AC2=BD2+BC2,
(3)2(1+cosα)AC2=k2BD2+BC2+2kBC•BDcosα.
理由:如图3,
延长BE至E'使BE'=AB,过点E'作E'D'∥ED交BD的延长线于D',
∴$\frac{BE}{BE'}=\frac{BD}{BD'}=\frac{DE}{D'E'}$,
∵AB=kBE,
∴D'E'=kDE,BD'=kBD,
∵AC=kDE,
∴D'E'=DE,
过点D'作D'H⊥BC于H,
∵∠CBD=α,
∴∠HBD'=180°-α,
∴BH=BD'cos(180°-α)=BD'cosα,HD'=BD'sinα,
延长CB至F使BF=BC,连接E'F,D'F,
同(1)的方法得出,△ABC≌△E'BF,
∴∠D'E'F=∠CBD=α,E'F=AC=D'E'
在Rt△FHD'中,FD'2=HD'2+FH2=HD'2+(BF-BH)2
=HD'2+BF2+BH2-2BF•BH
=(BD'sinα)2+BC2+(BD'cosα)2-2BC•BD'cosα
=(kBDsinα)2+BC2+(kBDcosα)2+2BC•kBDcosα
=k2BD2+BC2+2kBC•BDcosα,
过点D'作D'G⊥FE'交FE'于G,
同理:E'G=D'E'cosα,
FD'2=2D'E'2(1+cosα)=2AC2(1+cosα),
∴2(1+cosα)AC2=k2BD2+BC2+2kBC•BDcosα.
点评 此题相似形综合题,主要考查了全等三角形的判定和性质,相似三角形的性质和判定,勾股定理,锐角三角函数,解本题的关键是构造全等三角形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并写出这两条线段的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a>b,则ac>bc | |
| B. | 直线外一点与直线上各点连接的所有线段中,垂线段最短 | |
| C. | 相等的角是对顶角 | |
| D. | 同旁内角互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=b,大,7 | B. | a=b,小,7 | C. | a=-b,大,7 | D. | a=-b,小,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
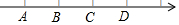 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别为整数a、b、c、d,且d-2a=4,则数轴的原点应是( )
如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别为整数a、b、c、d,且d-2a=4,则数轴的原点应是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com