
 如图,将矩形纸片ABCD折叠,使AB边与对角线AC重合,点B落在点F处,折痕为AE.若AD=8,EF=3,则AE的长为$3\sqrt{5}$.
如图,将矩形纸片ABCD折叠,使AB边与对角线AC重合,点B落在点F处,折痕为AE.若AD=8,EF=3,则AE的长为$3\sqrt{5}$. 分析 先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理求出AB的长,再根据勾股定理求出AE的长即可.
解答 解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8-3=5,
在Rt△CEF中,CF=$\sqrt{{CE}^{2}{-EF}^{2}}$=$\sqrt{{5}^{2}{-3}^{2}}$=4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,
∵AB=AF,AB=6,
∴AF=6,
又EF=3
∴AE=$\sqrt{{AF}^{2}{+EF}^{2}}$=$\sqrt{{6}^{2}{+3}^{2}}$=$3\sqrt{5}$
故答案为:$3\sqrt{5}$.
点评 此题考查的是翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x^2}+1}$=0 | B. | $\sqrt{1-x}$+$\frac{1}{3}$=0 | C. | $\sqrt{x+1}$=2 | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
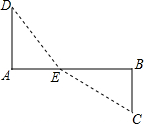 如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )
如图铁路上A,B两点相距40千米,C,D为两村庄,DA⊥AB,CB⊥AB,垂足分别为A和B,DA=24千米,CB=16千米.现在要在铁路旁修建一个煤栈E,使得C,D两村到煤栈的距离相等,那么煤栈E应距A点( )| A. | 20千米 | B. | 16千米 | C. | 12千米 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一次骰子,向上的一面是6点是必然事件 | |
| B. | 任意打开九年级下册数学教科书,正好是第97页是确定事件 | |
| C. | 购买一张彩票,中奖是不可能事件 | |
| D. | 如果a、b都是实数,那么a•b=b•a是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.6×106 | B. | 2.6×107 | C. | 0.26×108 | D. | 26×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2x+7 | B. | y=-2x-7 | C. | y=-2x-3 | D. | y=-2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com