
分析 (1)根据M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2}$代入n=5、50,即可求出M(5)、M(50) 的值;
(2)根据M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2}$代入数值即可得出2M(6)+M(7)和4M(7)+2M(8)的值;
(3)根据2016÷1008=2结合M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2}$即可求出2016M(n)+1008M(n+1)的值.
解答 解:(1)∵M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2}$,
∴M(5)=(-2)5=-32;M(50)=(-2)50=(-1)50×250=250.
故答案为:-32;正.
(2)①2M(6)+M(7)=2×(-2)6+(-2)7=27-27=0;
②4M(7)+2M(8)=4×(-2)7+2×(-2)8=-29+29=0.
(3)∵2016÷1008=2,
∴2016M(n)+1008M(n+1)=1008×(2M(n)+M(n+1))=1008×[-(-2)n+1+(-2)n+1]=0.
故答案为:0.
点评 本题考查了规律型中的数字的变化类,熟练运用M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2}$是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +14 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$.
如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
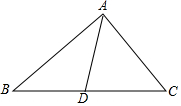 如图,在△ABC中,点D在BC上,在下列四个条件:①∠BAD=∠C;②∠ADC+∠BAC=180°; ③BA2=BD•BC;④$\frac{AB}{AD}$=$\frac{CB}{CA}$中能使△BDA∽△BAC的条件有( )
如图,在△ABC中,点D在BC上,在下列四个条件:①∠BAD=∠C;②∠ADC+∠BAC=180°; ③BA2=BD•BC;④$\frac{AB}{AD}$=$\frac{CB}{CA}$中能使△BDA∽△BAC的条件有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段AB=24,动点P从A出发,以2个单位/秒的速度沿射线AB运动,M为AP的中点.
如图,线段AB=24,动点P从A出发,以2个单位/秒的速度沿射线AB运动,M为AP的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com