
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.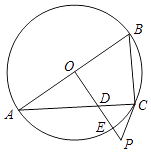
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把同样大小的黑色棋子摆放在正多边形的边上.第4个图形需要________________个棋子按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是_______________个(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
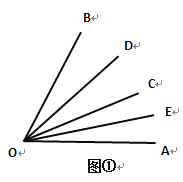
【题目】如图①,(1)∠AOB=60°,∠BOC=36°OD平分∠BOC,OE平分∠AOC,则∠EOD=____度;
(2)若∠AOB=90°,OD平分∠BOC,OE平分∠AOC,则∠EOD=__________;
(3)若∠AOB=α,其它条件同(2),则∠EOD=_________________.
类比应用:
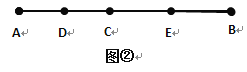
如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.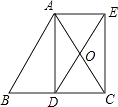
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣ ![]() ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
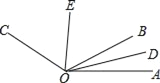
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)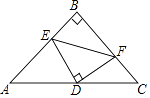
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B | b | 8 |
C | c | 5 |

(1)①在扇形图中,C部门所对应的圆心角的度数为
②在统计表中,b= , c=
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com