
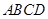 中,
中, 为
为 的中点,
的中点, 交
交 于点
于点 .
. ;
;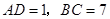 ,且
,且 平分
平分 时,求
时,求 的长.
的长.
 ,∴EF∥DM,又∵E为CD的中点∴F为CM中点即MF=CF,∴BF=BM+MF=AD+CF.
,∴EF∥DM,又∵E为CD的中点∴F为CM中点即MF=CF,∴BF=BM+MF=AD+CF. ,∴CE=EH=DE(角平分线上一点到角两边的距离相等),在Rt△ADE和Rt△AHE中,DE=EH,AE=AE∴Rt△ADE≌Rt△AHE(SH定理)∴AH=AD=1,同理可得BH=BC=7,∴AB=AH+BH=8∵四边形ABMD为平行四边形,∴DM=AB=8,又∵E、F分别为CD、CM中点,∴
,∴CE=EH=DE(角平分线上一点到角两边的距离相等),在Rt△ADE和Rt△AHE中,DE=EH,AE=AE∴Rt△ADE≌Rt△AHE(SH定理)∴AH=AD=1,同理可得BH=BC=7,∴AB=AH+BH=8∵四边形ABMD为平行四边形,∴DM=AB=8,又∵E、F分别为CD、CM中点,∴ .
.

 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 和
和 的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.
的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com