
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的内切圆
的内切圆![]() 与外接圆
与外接圆![]() 的周长之比为______.
的周长之比为______.
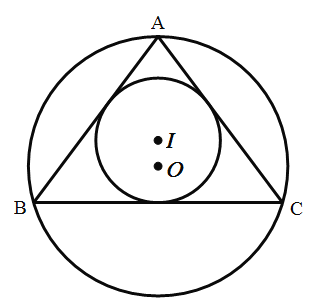
【答案】![]()
【解析】
过点A作AD⊥BC,过点E作EI⊥AB交AD于点I,过点F作AB的垂直平分线交AD于点O,再分别证△AEI∽△ADB和△AFO∽△ADB相似,求出EI和AO的长,再用圆的周长公式计算即可.
解:如图所示,
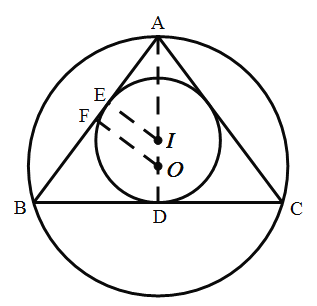
过点A作AD⊥BC,过点E作EI⊥AB交AD于点I,过点F作AB的垂直平分线交AD于点O,
∵![]() ,
,
∴EI,AO分别为内切圆![]() 与外接圆
与外接圆![]() 的半径,
的半径,
∵![]() ,
,
∴BD=3
∴AD=![]() ,
,
∵∠AEI=∠ADB,∠EAI=∠DAB,
∴△AEI∽△ADB,
∴![]() ,
,
∴EI=![]() ,
,
∵∠AFO=∠ADB,∠FAO=∠DAB,
∴△AFO∽△ADB,
∴![]()
∴AO=![]()
∴![]() 的内切圆
的内切圆![]() 与外接圆
与外接圆![]() 的周长之比为=(2π×
的周长之比为=(2π×![]() )∶(2π×
)∶(2π×![]() )=
)=![]() ,
,
故答案为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径![]() 米是其两腿迈出的步长之差
米是其两腿迈出的步长之差![]() 厘米
厘米![]() 的反比例函数,其图象如图所示.
的反比例函数,其图象如图所示.
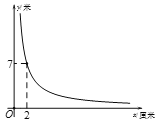
请根据图象中的信息解决下列问题:
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当某人两腿迈出的步长之差为![]() 厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
厘米时,他蒙上眼睛走出的大圆圈的半径为______米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于![]() 米,则其两腿迈出的步长之差最多是多少厘米?
米,则其两腿迈出的步长之差最多是多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线y=﹣2x2+bx+c过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D,抛物线的顶点为M,其对称轴交AB于点N.
(1)求抛物线的表达式及点M、N的坐标;
(2)是否存在点P,使四边形MNPD为平行四边形?若存在求出点P的坐标,若不存在,请说明理由.
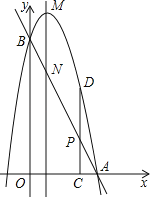
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市要选拔一名教师参加省级评优课比赛:经笔试、面试,结果小潘和小丁并列第一,评委会决定通过摸球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个蓝球,小潘先取出一个球,记住颜色后放回,然后小丁再取出一个球.若两次取出的球都是红球,则小潘胜出;若两次取出的球是一红一蓝,则小丁胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 为
为![]() 边上一点,满足
边上一点,满足![]() ,动点
,动点![]() 以
以![]() 的速度沿线段
的速度沿线段![]() 从点
从点![]() 移动到点
移动到点![]() ,连接
,连接![]() ,作
,作![]() ,交线段
,交线段![]() 于点
于点![]() ,设点
,设点![]() 移动的时间为
移动的时间为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
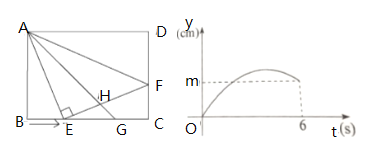
(1)图①中,![]() _______
_______![]() ,图②中,
,图②中,![]() _______;
_______;
(2)点![]() 能否为线段
能否为线段![]() 的中点?若可能,求出此时
的中点?若可能,求出此时![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
(3)在图①中,连接![]() 、
、![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() 平分
平分![]() 的面积,求此时
的面积,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,ABAF=ACAE.
(1)求证:∠AFD=∠AEC;
(2)若EG∥CD,交边AC的延长线于点G,求证:CDCG=FCBD.
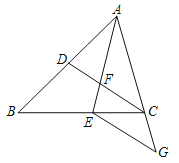
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点A(2,6).
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限?y随x的增大如何变化?
(3)点B(3,4),C(5,2),D(![]() ,
,![]() )是否在这个函数图象上?为什么?
)是否在这个函数图象上?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x+2)(x﹣4)与x轴交于A,B两点,与y轴交于点C,且∠ACO=∠CBO.
(1)求线段OC的长度;
(2)若点D在第四象限的抛物线上,连接BD、CD,求△BCD的面积的最大值;
(3)若点P在平面内,当以点A、C、B、P为顶点的四边形是平行四边形时,直接写出点P的坐标.
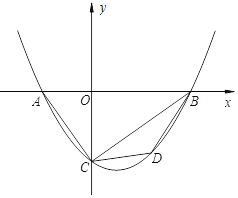
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com