
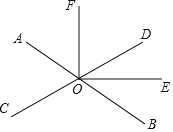
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ![]() ,﹣2);⑤当x<
,﹣2);⑤当x< ![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )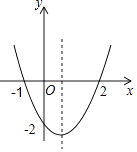
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 . 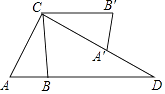
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)= ![]() .
.
例如:tan15°=tan(45°﹣30°)= ![]() =
= 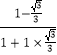 =
= ![]()
= ![]() =
= ![]() =2﹣
=2﹣ ![]() .
.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据 ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)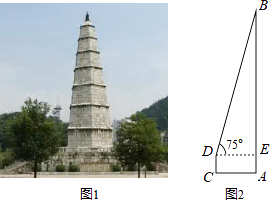
查看答案和解析>>
科目:初中数学 来源: 题型:
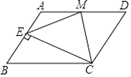
【题目】如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.
(1)求平行四边形ABCD的面积S;
(2)求证:∠EMC=2∠AEM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
(1)试证明:DE=BF;
(2)连接DF,BE,猜想DF与BE的关系?并证明你的猜想的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com