
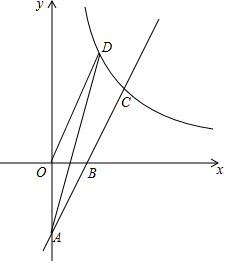
 如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.
如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.分析 (1)在y=kx-4(k≠0)中,当x=0时y=-1,可求A的坐标,再在Rt△ABO中,根据三角函数可求B的坐标,根据待定系数法及可求得结论;
(2)先求出D点坐标,再根据三角形面积公式即可求得结论.
解答  解:(1)在y=kx-4(k≠0)中,当x=0时y=-1,
解:(1)在y=kx-4(k≠0)中,当x=0时y=-1,
∴A(0,-4),
在Rt△ABO中:tan∠OAB=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴OB=2,
∴B(2,0),
将B(2,0)代入y=kx-4(k≠0)中:k=2,
∴y=2x-4,
当x=4时,y=4,
∴C(4,4),
∴m=4×4=16,
∴y=$\frac{16}{x}$;
(2)当y=6时,x=$\frac{8}{3}$,
∴D($\frac{8}{3}$,6),
∴S=$\frac{1}{2}$×4×$\frac{8}{3}$=$\frac{16}{3}$.
点评 此题考查了待定系数法求函数解析式,反比例函数与一次函数的交点问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=-$\frac{1}{x}$ | D. | y=2x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.
如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>$\frac{1}{2}$ | B. | k<$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | 不存在 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com