
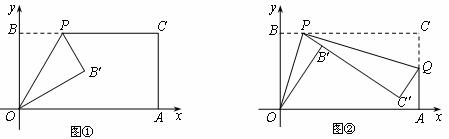
已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′ 和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′ 恰好落在边OA上时,求点P的坐标(直接写出结果即可).
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的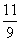 ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
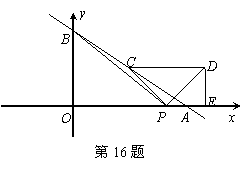
如图:直线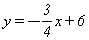 与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值:
与x,y轴分别交于A,B,C是AB的中点,点P从A出发以每秒1个单位的速度沿射线AO方向运动,将点C绕P顺时针旋转90°得到点D,作DE⊥x轴,垂足为E,连接PC,PD,PB.设点P的运动时间为t秒(0≤t≤16),当以P,D,E为顶点的三角形与△BOP相似时,写出所有t的值:
查看答案和解析>>
科目:初中数学 来源: 题型:
已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)
为□ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵
坐标都是整数的点,则N(t)所有可能的值为 ( )
A.6、7 B.7、8 C.6、7、8 D.6、8、9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com