

科目:初中数学 来源: 题型:解答题
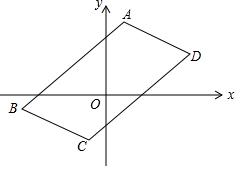 图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点
图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某路口每天在学校放学时段的车流量 | |
| B. | 检测某种新型LED灯的使用寿命 | |
| C. | 检测站对本市所有公交车的年度安全检查 | |
| D. | 了解同一批青菜的农药残留量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
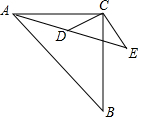 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
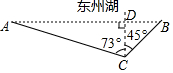 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.
某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com