
分析 (1)根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可;
(2)经济时速就是耗油量最小的行驶速度.
解答 解:(1)∵汽车在每小时90~150公里之间行驶时(含90公里和150公里),每公里耗油($\frac{1}{21}$+$\frac{525}{{x}^{2}}$)升.
∴y=x×($\frac{1}{21}$+$\frac{525}{{x}^{2}}$)=$\frac{x}{21}$+$\frac{525}{x}$(90≤x≤150);
(2)根据材料得:当$\frac{x}{21}$=$\frac{525}{x}$时有最小值,
解得:x=105,
∴该汽车的经济时速为105千米/小时;
当x=105时百公里耗油量为100×($\frac{1}{21}$+$\frac{525}{105×105}$)≈9.5(升).
答:每百公里的耗油量为9.5升.
点评 本题考查了反比例函数的应用,解题的关键是读懂题目提供的材料,易错点是了解“耗油总量=每公里的耗油量×行驶的速度”,难度中等偏上.


科目:初中数学 来源: 题型:解答题
 已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M
已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3-\sqrt{5}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
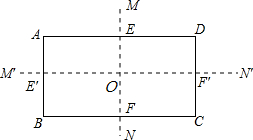 如图,MN、M′N′都是长方形的对称轴,回答下列问题:
如图,MN、M′N′都是长方形的对称轴,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com