
| A. | a=3,b=6,c=2,d=4 | B. | $a=1,b=\sqrt{2},c=\sqrt{6},d=\sqrt{3}$ | ||
| C. | $a=2,b=\sqrt{5},c=\sqrt{15},d=2\sqrt{3}$ | D. | a=4,b=6,c=5,d=10 |
科目:初中数学 来源: 题型:填空题
 如图,经过坐标原点O的直线AB与双曲线y=$\frac{-3}{x}$相交于A,B两点,BC⊥x轴于点C,连结AC,则△AOC的面积为$\frac{3}{2}$.
如图,经过坐标原点O的直线AB与双曲线y=$\frac{-3}{x}$相交于A,B两点,BC⊥x轴于点C,连结AC,则△AOC的面积为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
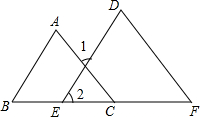 如图填空:
如图填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影画),并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是30m,求小华家到公路的距离.
如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区(用阴影画),并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是30m,求小华家到公路的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?
已知:如图,O点在△ABC内部,连AO、BO、CO,A′、B′、C′分别在AO、BO、CO上,且AB∥A′B′、BC∥B′C′.图中△OAC与△OA′C′相似吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com