
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy= ![]() x2+mx+n”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨≈◊ŒÔœþµƒ∂‘≥∆÷·Ωªx÷·”⁄µ„D£¨“—÷™A(1£¨0)£¨C(0£¨2)£Æ
x2+mx+n”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨≈◊ŒÔœþµƒ∂‘≥∆÷·Ωªx÷·”⁄µ„D£¨“—÷™A(1£¨0)£¨C(0£¨2)£Æ
(1)«Û≈◊ŒÔœþµƒ±Ì¥Ô Ω£ª
(2) «Îƒ„‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ’“µ„P£¨ π°˜PCD «“‘CDŒ™—¸µƒµ»—¸»˝Ω«–Œ£¨À˘”–∑˚∫œÃıº˛µƒµ„Pµƒ◊¯±Í∑÷±Œ™ £ª
(3)µ„E «œþ∂ŒBC…œµƒ“ª∏ˆ∂ص„£¨π˝µ„E◊˜x÷·µƒ¥πœþ”Î≈◊ŒÔœþœýΩª”⁄µ„F£¨µ±µ„E‘À∂ØµΩ ≤√¥Œª÷√ ±£¨Àƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û?«Û≥ˆÀƒ±þ–ŒCDBFµƒ◊Ó¥Û√ʪ˝º∞¥À ±Eµ„µƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©y=©Å![]() x2+
x2+![]() x+2£ª£®2£©P1£®
x+2£ª£®2£©P1£®![]() £¨4£©£¨P2£®
£¨4£©£¨P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Å
£¨©Å![]() £©£ª£®3£©SÀƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û=
£©£ª£®3£©SÀƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û=![]() £¨E£®2£¨1£©
£¨E£®2£¨1£©
°æΩ‚Œˆ°ø
£®1£©÷±Ω”∞—Aµ„∫ÕCµ„◊¯±Í¥˙»Îy=©Å![]() x2+mx+nµ√m°¢nµƒ∑Ω≥Ã◊È£¨»ª∫ÛΩ‚∑Ω≥Ã◊È«Û≥ˆm°¢nº¥ø…µ√µΩ≈◊ŒÔœþΩ‚Œˆ Ω£ª
x2+mx+nµ√m°¢nµƒ∑Ω≥Ã◊È£¨»ª∫ÛΩ‚∑Ω≥Ã◊È«Û≥ˆm°¢nº¥ø…µ√µΩ≈◊ŒÔœþΩ‚Œˆ Ω£ª
£®2£©œ»¿˚”√≈◊ŒÔœþ∂‘≥∆÷·∑Ω≥ëÛ≥ˆ≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™÷±œþx=©Å![]() £¨‘ÚD£®
£¨‘ÚD£®![]() £¨0£©£¨‘Ú¿˚”√π¥π…∂®¿Ìº∆À„≥ˆCD=
£¨0£©£¨‘Ú¿˚”√π¥π…∂®¿Ìº∆À„≥ˆCD=![]() £¨»ª∫Û∑÷¿ýÃ÷¬€£∫»ÁÕº1£¨µ±CP=CD ±£¨¿˚”√µ»—¸»˝Ω«–Œµƒ–‘÷ “◊µ√P1£®
£¨»ª∫Û∑÷¿ýÃ÷¬€£∫»ÁÕº1£¨µ±CP=CD ±£¨¿˚”√µ»—¸»˝Ω«–Œµƒ–‘÷ “◊µ√P1£®![]() £¨4£©£ªµ±DP=DC ±£¨“◊µ√P2£®
£¨4£©£ªµ±DP=DC ±£¨“◊µ√P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
£®3£©œ»∏˘æð≈◊ŒÔœþ”Îx÷·µƒΩªµ„Œ «Û≥ˆB£®4£¨0£©£¨‘Ÿ¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œþBCµƒΩ‚Œˆ ΩŒ™y=©Å![]() x+2£¨¿˚”√“ª¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜∫Õ∂˛¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜£¨…ËE£®x£¨©Å
x+2£¨¿˚”√“ª¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜∫Õ∂˛¥Œ∫Ø ˝ÕºœÛ…œµ„µƒ◊¯±ÍÃÿ’˜£¨…ËE£®x£¨©Å![]() x+2£©£®0°Ðx°Ð4£©£¨‘ÚF£®x£¨©Å
x+2£©£®0°Ðx°Ð4£©£¨‘ÚF£®x£¨©Å![]() x2+
x2+![]() x+2£©£¨‘ÚFE=©Å
x+2£©£¨‘ÚFE=©Å![]() x2+2x£¨”…”⁄°˜BEF∫Õ°˜CEFπ≤µ◊±þ£¨∏þµƒ∫ÕŒ™4£¨‘ÚS°˜BCF=S°˜BEF+S°˜CEF=
x2+2x£¨”…”⁄°˜BEF∫Õ°˜CEFπ≤µ◊±þ£¨∏þµƒ∫ÕŒ™4£¨‘ÚS°˜BCF=S°˜BEF+S°˜CEF=![]() 4EF=©Åx2+4x£¨º”…œS°˜BCD=
4EF=©Åx2+4x£¨º”…œS°˜BCD=![]() £¨À˘“‘SÀƒ±þ–ŒCDBF=S°˜BCF+S°˜BCD=©Åx2+4x+
£¨À˘“‘SÀƒ±þ–ŒCDBF=S°˜BCF+S°˜BCD=©Åx2+4x+![]() £®0°Ðx°Ð4£©£¨»ª∫Û∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ «ÛÀƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û£¨≤¢µ√µΩ¥À ±Eµ„◊¯±Í£Æ
£®0°Ðx°Ð4£©£¨»ª∫Û∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ «ÛÀƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û£¨≤¢µ√µΩ¥À ±Eµ„◊¯±Í£Æ
£®1£©°þ≈◊ŒÔœþy=©Å![]() x2+mx+næ≠π˝A£®©Å1£¨0£©£¨C£®0£¨2£©£Æ
x2+mx+næ≠π˝A£®©Å1£¨0£©£¨C£®0£¨2£©£Æ
°ý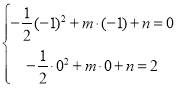 Ω‚µ√£∫
Ω‚µ√£∫ £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™£∫y=©Å![]() x2+
x2+![]() x+2£ª
x+2£ª
£®2£©≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™÷±œþ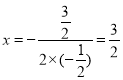 £¨‘ÚD£®
£¨‘ÚD£®![]() £¨0£©£¨
£¨0£©£¨
°ý![]() £¨
£¨
»ÁÕº1£¨
µ±CP=CD ±£¨‘ÚP1£®![]() £¨4£©£ª
£¨4£©£ª
µ±DP=DC ±£¨‘ÚP2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Å
£¨©Å![]() £©£¨
£©£¨
◊€…œÀ˘ ˆ£¨¬˙◊„Ãıº˛µƒPµ„◊¯±ÍŒ™P1£®![]() £¨4£©£¨P2£®
£¨4£©£¨P2£®![]() £¨
£¨![]() £©£¨P3£®
£©£¨P3£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
£®3£©µ±y=0 ±£¨0=©Å![]() x2+
x2+![]() x+2
x+2
°ýx1=©Å1£¨x2=4£¨°ýB£®4£¨0£©£Æ
…Ë÷±œþBCµƒΩ‚Œˆ ΩŒ™y=kx+b£¨”…ÕºœÛ£¨µ√
![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫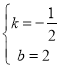 £¨
£¨
°ý÷±œþBCµƒΩ‚Œˆ ΩŒ™£∫y=©Å![]() x+2£Æ
x+2£Æ
»ÁÕº2£¨π˝µ„C◊˜CM°ÕEF”⁄M£¨

…ËE£®a£¨©Å![]() a+2£©£¨F£®a£¨©Å
a+2£©£¨F£®a£¨©Å![]() a2+
a2+![]() a+2£©£¨
a+2£©£¨
°ýEF=©Å![]() a2+
a2+![]() a+2©Å£®©Å
a+2©Å£®©Å![]() a+2£©=©Å
a+2£©=©Å![]() a2+2a£®0°Ðx°Ð4£©£Æ
a2+2a£®0°Ðx°Ð4£©£Æ
°þSÀƒ±þ–ŒCDBF=S°˜BCD+S°˜CEF+S°˜BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN£¨
EFBN£¨
=![]() +
+![]() a£®©Å
a£®©Å![]() a2+2a£©+
a2+2a£©+![]() £®4©Åa£©£®©Å
£®4©Åa£©£®©Å![]() a2+2a£©£¨
a2+2a£©£¨
=©Åa2+4a+![]() £®0°Ðx°Ð4£©£Æ=©Å£®a©Å2£©2+
£®0°Ðx°Ð4£©£Æ=©Å£®a©Å2£©2+![]()
°ýa=2 ±£¨SÀƒ±þ–ŒCDBFµƒ√ʪ˝◊Ó¥Û=![]() £¨
£¨
°ýE£®2£¨1£©£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=©Åx2©Å2x+3 µƒÕºœÛ”Îx÷·Ωª”⁄A°¢B¡Ωµ„(µ„A‘⁄µ„Bµƒ◊Û±þ)£¨”Îy÷·Ωª”⁄µ„C£Æ
£®1£©«ÛA°¢B°¢Cµƒ◊¯±Í£ª
£®2£©π˝≈◊ŒÔœþ…œ“ªµ„F◊˜y÷·µƒ∆Ω––œþ£¨”Î÷±œþACΩª”⁄µ„G£Æ»ÙFG=![]() AC£¨«Ûµ„Fµƒ◊¯±Í£ª
AC£¨«Ûµ„Fµƒ◊¯±Í£ª
£®3£©E(0,©Å2)£¨¡¨Ω”BE£ÆΩ´°˜OBE»∆∆Ω√ʃ⁄µƒƒ≥µ„ƒÊ ±’Ζ˝◊™90°„µ√µΩ°˜O°‰B°‰E°‰£¨O°¢B°¢Eµƒ∂‘”¶µ„∑÷±Œ™O°‰°¢B°‰°¢E°‰£Æ»Ùµ„B°‰°¢E°‰¡Ωµ„«°∫√¬‰‘⁄≈◊ŒÔœþ…œ£¨«Ûµ„B°‰µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
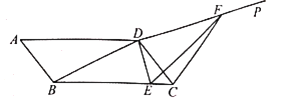
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨∂‘Ω«œþ
£¨∂‘Ω«œþ![]() £¨µ„E «œþ∂ŒBC…œµƒ∂ص„£¨¡¨Ω”DE£¨π˝µ„D◊˜DP°ÕDE£¨‘⁄…‰œþDP…œ»°µ„F£¨ πµ√
£¨µ„E «œþ∂ŒBC…œµƒ∂ص„£¨¡¨Ω”DE£¨π˝µ„D◊˜DP°ÕDE£¨‘⁄…‰œþDP…œ»°µ„F£¨ πµ√![]() £¨¡¨Ω”CF,‘Ú
£¨¡¨Ω”CF,‘Ú![]() ÷Ð≥§µƒ◊Ó–°÷µŒ™___________.
÷Ð≥§µƒ◊Ó–°÷µŒ™___________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒ÷±æ∂£¨µ„
µƒ÷±æ∂£¨µ„![]() £¨
£¨![]() «
«![]() …œ¡Ωµ„£¨«“
…œ¡Ωµ„£¨«“![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() Ωª
Ωª![]() —”≥§œþ”⁄µ„
—”≥§œþ”⁄µ„![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £Æ
£Æ
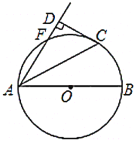
£®1£©«Û÷§£∫![]() «
«![]() µƒ«–œþ£ª
µƒ«–œþ£ª
£®2£©»Ù![]() £¨«Û
£¨«Û![]() µƒ∞Îæ∂£Æ
µƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
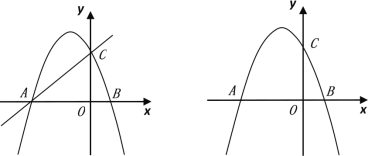
°æƒø°øœ÷”–A°¢B¡Ω∏ˆ≤ªÕ∏√˜¥¸◊”£¨∑÷±◊∞”–3∏ˆ≥˝—’…´Õ‚ÕÍ»´œýÕ¨µƒ–°«Ú£Æ∆‰÷–£¨A¥¸◊∞”–2∏ˆ∞◊«Ú£¨1∏ˆ∫Ï«Ú£ªB¥¸◊∞”–2∏ˆ∫Ï«Ú£¨1∏ˆ∞◊«Ú£Æ
(1)Ω´A¥¸“°‘»£¨»ª∫Û¥”A¥¸÷–Àʪ˙»°≥ˆ“ª∏ˆ–°«Ú£¨‘Ú√˛≥ˆ–°«Ú «∞◊…´µƒ∏≈¬ Œ™ £ª
(2)–°ª™∫Õ–°¡÷…Ã∂®¡À“ª∏ˆ”Œœ∑πÊ‘Ú£∫¥”“°‘»∫ÛµƒA£¨B¡Ω¥¸÷–Àʪ˙√˛≥ˆ“ª∏ˆ–°«Ú£¨√˛≥ˆµƒ’‚¡Ω∏ˆ–°«Ú£¨»Ù—’…´œýÕ¨£¨‘Ú–°¡÷ªÒ §£ª»Ù—’…´≤ªÕ¨£¨‘Ú–°ª™ªÒ §£Æ«Î”√¡–±ÌªÚª≠≥ˆ ˜◊¥Õºµƒ∑Ω∑®Àµ√˜’‚∏ˆ”Œœ∑πÊ‘Ú∂‘À´∑Ω «∑Òπ´∆Ω£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨”√≥§33√◊µƒ÷Ò¿È∞ Œß≥…“ª∏ˆæÿ–Œ‘∫«Ω£¨∆‰÷–“ª√Êøø«Ω£¨«Ω≥§15√◊£¨«Ωµƒ∂‘√Ê”–“ª∏ˆ2√◊ø̵ƒ√≈£¨…Ë¥π÷±”⁄«Ωµƒ“ª±þ≥§Œ™![]() √◊£¨‘∫«Ωµƒ√ʪ˝Œ™
√◊£¨‘∫«Ωµƒ√ʪ˝Œ™![]() ∆Ω∑Ω√◊£Æ
∆Ω∑Ω√◊£Æ
£®1£©÷±Ω”–¥≥ˆ![]() ”Î
”Î![]() µƒ∫Ø ˝πÿœµ Ω£ª
µƒ∫Ø ˝πÿœµ Ω£ª
£®2£©»Ù‘∫«Ωµƒ√ʪ˝Œ™143∆Ω∑Ω√◊£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©»Ù‘⁄«Ωµƒ∂‘√Ê‘Ÿø™“ª∏ˆøÌŒ™![]() √◊µƒ√≈£¨«“√ʪ˝
√◊µƒ√≈£¨«“√ʪ˝![]() µƒ◊Ó¥Û÷µŒ™165∆Ω∑Ω√◊£¨«Û
µƒ◊Ó¥Û÷µŒ™165∆Ω∑Ω√◊£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨æÿ–ŒABCD÷–£¨AB£Ω4cm£¨BC£Ω8cm£¨ACµƒ¥π÷±∆Ω∑÷œþEF∑÷±ΩªAD°¢BC”⁄µ„E°¢F£¨¥π◊„Œ™O£Æ
£®1£©»ÁÕº£®1£©£¨¡¨Ω”AF°¢CE£Æ
¢ŸÀƒ±þ–ŒAFCE « ≤√¥Ãÿ ‚Àƒ±þ–Œ£øÀµ√˜¿Ì”…£ª
¢⁄«ÛAFµƒ≥§£ª
£®2£©»ÁÕº£®2£©£¨∂ص„P°¢Q∑÷±¥”A°¢C¡Ωµ„Õ¨ ±≥ˆ∑¢£¨—ÿ°˜AFB∫Õ°˜CDE∏˜±þ‘»ÀŸ‘À∂Ø“ª÷Уƺ¥µ„P◊‘A°˙F°˙B°˙AÕ£÷𣨵„Q◊‘C°˙D°˙E°˙CÕ£÷π£Æ‘⁄‘À∂Øπ˝≥Ã÷–£¨“—÷™µ„PµƒÀŸ∂»Œ™√ø√Î5cm£¨µ„QµƒÀŸ∂»Œ™√ø√Î4cm£¨‘À∂Ø ±º‰Œ™t√Σ¨µ±A°¢C°¢P°¢QÀƒµ„Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ ±£¨«Ûtµƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
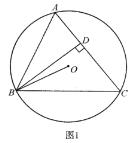
°æƒø°ø![]() ƒ⁄Ω””⁄
ƒ⁄Ω””⁄![]() ±þ”⁄µ„
±þ”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
![]() »ÁÕº1£¨«Û÷§:
»ÁÕº1£¨«Û÷§:![]() £ª
£ª
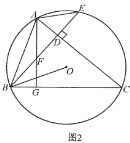
![]() »ÁÕº2£¨—”≥§
»ÁÕº2£¨—”≥§![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨µ„
£¨µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£¨…‰œþ
…œ£¨…‰œþ![]() Ωª
Ωª![]() ±þ”⁄µ„
±þ”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() £¨«Û÷§:
£¨«Û÷§:![]() £ª
£ª
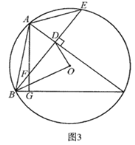
![]() »ÁÕº3£¨‘⁄
»ÁÕº3£¨‘⁄![]() µƒÃıº˛œ¬£¨¡¨Ω”
µƒÃıº˛œ¬£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨«Ûœþ∂Œ
£¨«Ûœþ∂Œ![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþy=£≠x2+mx+3”Îx÷·Ωª”⁄µ„A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄Cµ„£¨µ„Bµƒ◊¯±ÍŒ™£®3£¨0£©£¨≈◊ŒÔœþ”Î÷±œþy=£≠![]() x+3Ωª”⁄C°¢D¡Ωµ„£Æ¡¨Ω”BD°¢AD£Æ
x+3Ωª”⁄C°¢D¡Ωµ„£Æ¡¨Ω”BD°¢AD£Æ
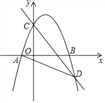
£®1£©«Ûmµƒ÷µ£Æ
£®2£©≈◊ŒÔœþ…œ”–“ªµ„P£¨¬˙◊„S°˜ABP=4S°˜ABD£¨«Ûµ„Pµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com