
 ��ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ��-4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s����
��ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ��-4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s�������� ��1����֤��BAP�ա�PQD���Ӷ��õ�DQ=AP=t���Ӷ����������PBD�Ķ����͵�D�����ꣻ
��2�����ڡ�EBP=45�㣬��ͼ1����������Ϊ������һ������ͼ�Σ����õ�EP=AP+CE�����õ���POE�ܳ�����AO+CO=8���Ӷ�������⣻
��3��EP=AP+CE�����ڡ�PBE�ױ߲������ʷ�����������ۣ�������������ȫ�ȼ����ɶ���������⣬Ȼ������������ȡ�ᣬ����ȷ������Ҫ���tֵ��
��� �⣺��1����ͼ1��
����ɵã�AP=OQ=1��t=t���룩
��AO=PQ��
���ı���OABC�������Σ�
��AO=AB=BC=OC��
��BAO=��AOC=��OCB=��ABC=90�㣮
��DP��BP��
���BPD=90�㣮
���BPA=90��-��DPQ=��PDQ��
��AO=PQ��AO=AB��
��AB=PQ��
�ڡ�BAP�͡�PQD�У�
$\left\{\begin{array}{l}{��BAP=��PQD\\;}\\{��BPA=��PDQ}\\{AB=PQ}\end{array}\right.$
���BAP�ա�PQD��AAS����
��AP=QD��BP=PD��
�ߡ�BPD=90�㣬BP=PD��
���PBD=��PDB=45�㣮
��AP=t��
��DQ=t��
���D������t��t����
�ʴ�Ϊ��45�㣬��t��t����
��2���ӳ�OA����F��ʹ��AF=CE������BF����ͼ2��ʾ��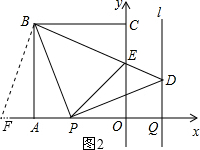 �ڡ�FAB�͡�ECB�У�
�ڡ�FAB�͡�ECB�У�
$\left\{\begin{array}{l}{AB=CB}\\{��BAF=��BCE=90��}\\{AF=CE}\end{array}\right.$
���FAB�ա�ECB��
��FB=EB����FBA=��EBC��
�ߡ�EBP=45�㣬��ABC=90�㣬
���ABP+��EBC=45�㣮
���FBP=��FBA+��ABP
=��EBC+��ABP=45�㣮
���FBP=��EBP��
�ڡ�FBP�͡�EBP�У�
$\left\{\begin{array}{l}{BF=BE}\\{��FBP=��EBP}\\{BP=BP}\end{array}\right.$
���FBP�ա�EBP��SAS����
��FP=EP�� �ߡ�EBP=45�㣬
�ߡ�EBP=45�㣬
����ͼ1���Եõ�EP=CE+AP��
��OP+PE+OE=OP+AP+CE+OE
=AO+CO
=4+4
=8��
���POE�ܳ��Ƕ�ֵ���ö�ֵΪ8��
��3������PB=PE��
�ɡ�PAB�ա�DQP��PB=PD��
��ȻPB��PE��
���������Ӧ��ȥ��
����EB=EP��
���PBE=��BPE=45�㣮
���BEP=90�㣮
���PEO=90��-��BEC=��EBC��
�ڡ�POE�͡�ECB�У�
$\left\{\begin{array}{l}{��PEO=��EBC}\\{��POE=��ECB}\\{EP=BE}\end{array}\right.$
���POE�ա�ECB��AAS����
��OE=CB=OC��
���E���C�غϣ�EC=0����
���P���O�غϣ�PO=0����
�ߵ�B��-4��4����
��AO=CO=4��
��ʱt=AP=AO=4��
����BP=BE��
��Rt��BAP��Rt��BCE��
$\left\{\begin{array}{l}{BA=BC}\\{BP=BE}\end{array}\right.$
��Rt��BAP��Rt��BCE��HL����
��AP=CE��
��AP=t��
��CE=t��
��PO=EO=4-t��
�ߡ�POE=90�㣬
��PE=$\sqrt{P{O}^{2}+E{O}^{2}}$=$\sqrt{2}$��4-t����
�ɣ�2����EP=FP=FA+AP=CE+AP��
��EP=t+t=2t��
��$\sqrt{2}$��4-t��=2t��
��ã�t=4$\sqrt{2}$-4
�൱tΪ4���4$\sqrt{2}$-4����ʱ����PBEΪ���������Σ�
���� ���⿼���������ε����ʡ����������ε����ʡ�ȫ�������ε��������ж������ɶ�����֪ʶ�������˷������۵�˼�룬���������û����������������������ۺ��Էdz�ǿ����Ϥ��������һ������Ϊ45��Ľ���ɵĻ���ͼ�Σ����нǵĶ����������ε�һ�������غϣ��ǵ������������ε����߷ֱ��ཻ���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
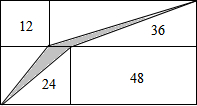 ��ͼ���������ĸ�����ֱ�Ϊ12cm2��36cm2��24cm2��48cm2��С������ƴ�ɣ���ͼ����Ӱ���ֵ�����Ƕ���cm2��
��ͼ���������ĸ�����ֱ�Ϊ12cm2��36cm2��24cm2��48cm2��С������ƴ�ɣ���ͼ����Ӱ���ֵ�����Ƕ���cm2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
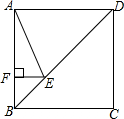 ��ͼ��������ABCD�ı߳�Ϊ4����E�ڶԽ���BD�ϣ��ҡ�BAE=22.5�㣬EF��AB������ΪF����EF�ij�Ϊ��������
��ͼ��������ABCD�ı߳�Ϊ4����E�ڶԽ���BD�ϣ��ҡ�BAE=22.5�㣬EF��AB������ΪF����EF�ij�Ϊ��������| A�� | 4-2$\sqrt{2}$ | B�� | 3$\sqrt{2}$-4 | C�� | 1 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
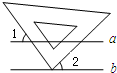 ��ͼ��ֱ��a��ֱ��b����һ���������ǰ��ֱ�Ƕ������ֱ��b�ϣ�����2=34�㣬���1=56�㣮
��ͼ��ֱ��a��ֱ��b����һ���������ǰ��ֱ�Ƕ������ֱ��b�ϣ�����2=34�㣬���1=56�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com