
 在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.分析 (1)将A、B点的坐标代入y=ax2+bx+4得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)连接BQ交直线x=$\frac{1}{2}$于点M,对称轴交x轴于E点,如图1,先利用两点坐标线段最短得到此时MA+MQ的值最小,再利用垂线段最短得到当BQ⊥AC时,BQ最短,则MA+MQ最小,然后证明Rt△BME∽Rt△CAO,利用相似比计算出ME,从而可确定M点坐标;
(3)连接CP、BC,如图,由BC=BD得到∠BDC=∠BCD,再由线段PQ被CD垂直平分得到DQ=DP,∠QDC=∠PDC,则∠QDC=∠BCD,所以DQ∥BC,则可证明△ADQ∽△ABC,然后利用相似比计算出DQ,从而得到AP的长,最后利用速度公式计算t的值.
解答 解:(1)将A、B点的坐标代入y=ax2+bx+4得$\left\{\begin{array}{l}{9a-3b+4=0}\\{16a+4b+4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$,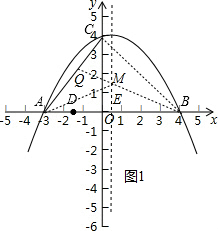
所以抛物线的解析式为y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4;
(2)当x=0时,y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4=4,则C(0,4),抛物线的对称轴为直线x=-$\frac{b}{2a}$=$\frac{1}{2}$,
连接BQ交直线x=$\frac{1}{2}$于点M,对称轴交x轴于E点,如图1,则MA=MB,
∴MA+MQ=MB+MQ=BQ,
此时MA+MQ的值最小,
当BQ⊥AC时,BQ最短,则MA+MQ最小,
∵∠QBA+∠QAB=90°,∠CAO+∠ACO=90°,
∴∠ACO=∠QBA,
∴Rt△BME∽Rt△CAO,
∴ME:AO=BE:OC,即ME:3=$\frac{7}{2}$:4,解得ME=$\frac{21}{8}$,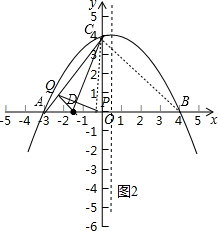
∴M点坐标为($\frac{1}{2}$,$\frac{21}{8}$);
(3)存在.
连接CP、BC,如图,
∴B(-4,0),C(0,4),
∴BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵BC=BD=4$\sqrt{2}$
∴∠BDC=∠BCD,AD=AB-BD=7-4$\sqrt{2}$,
∵线段PQ被CD垂直平分,
∴DQ=DP,∠QDC=∠PDC,
∴∠QDC=∠BCD,
∴DQ∥BC,
∴△ADQ∽△ABC,
∴DQ:BC=AD:AB,即DQ:4$\sqrt{2}$=(7-4$\sqrt{2}$):7,解得DQ=$\frac{28\sqrt{2}-32}{7}$,
∴DP=$\frac{28\sqrt{2}-32}{7}$,
∴AP=AD+DP=7-4$\sqrt{2}$+$\frac{28\sqrt{2}-32}{7}$=$\frac{17}{7}$,
∴t=$\frac{17}{7}$÷1=$\frac{17}{7}$,
即t的值是$\frac{17}{7}$秒.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和垂直平分线的性质;会运用待定系数法求二次函数解析式;理解坐标与图形性质;会运用相似比计算线段的长;能利用两点之间线段最短和垂线段最短解决最短路径问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
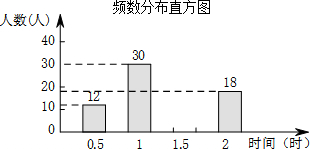 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:| 劳动时间(时) | 频数 |
| 0.5 | 12 |
| 1 | 30 |
| 1.5 | m |
| 2 | 18 |
| 合计 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com