
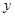 轴相切于坐标原点O(0,0),与
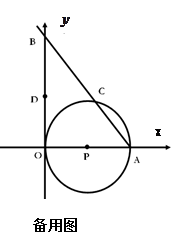
轴相切于坐标原点O(0,0),与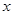 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与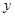 轴的正半轴交于点B,与⊙P交于点C.
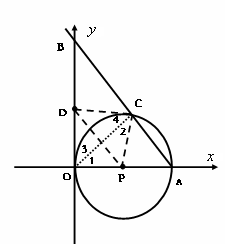
轴的正半轴交于点B,与⊙P交于点C.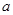 , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同 ,函数
,函数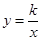 的图象经过点
的图象经过点 ,求
,求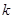 的值(用含
的值(用含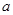 的代数式表示).
的代数式表示). 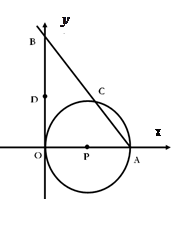
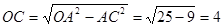 ,
,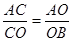 ,即
,即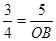 ,
,  , ∴
, ∴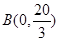
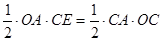 ,
,
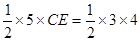 ,∴
,∴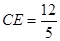 ,
,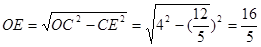 ∴
∴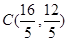 ,
,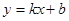 .
.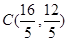 代入上式得:
代入上式得: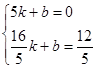 , 解得:
, 解得: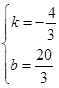 ,
,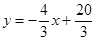 , ∴点
, ∴点 .4分
.4分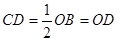 ,
,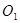 是DP的中点,圆心
是DP的中点,圆心 ,
,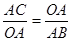 ,求得:AB=
,求得:AB=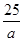 ,在Rt△ABO中,
,在Rt△ABO中,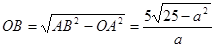 ,OD=
,OD=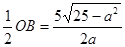 ,
,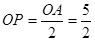
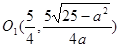 ,点
,点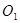 在函数
在函数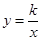 的图象上,
的图象上, , ∴
, ∴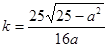
 .
.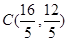 代入上式解得即可.
代入上式解得即可.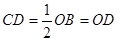 ,求证Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形,可得PD上的中点到点O、P、C、D四点的距离相等,由上可知,经过点O、P、C、D的圆心O1是DP的中点,圆心
,求证Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形,可得PD上的中点到点O、P、C、D四点的距离相等,由上可知,经过点O、P、C、D的圆心O1是DP的中点,圆心 ,由(1)知:Rt△AOC∽Rt△ABO,可得
,由(1)知:Rt△AOC∽Rt△ABO,可得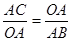 ,求得:AB、OD即可.
,求得:AB、OD即可.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
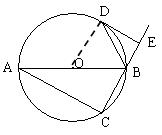
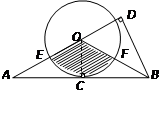
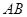 是⊙O的直径,
是⊙O的直径,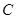 为
为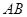 延长线上的一点,
延长线上的一点,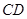 交⊙O于点
交⊙O于点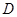 ,且
,且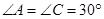 .
. 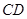 是⊙O的切线;
是⊙O的切线;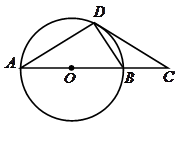
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
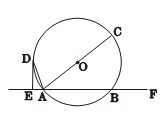
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com