
【题目】(11分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
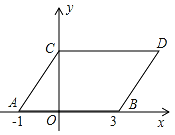
(1)求点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
①若P在线段BD之间时(不与B,D重合),求S△CDP+S△BOP的取值范围;
②若P在直线BD上运动,请直接写出∠CPO、∠DCP、∠BOP的数量关系.
【答案】(1)C(0,2),D(4,2);(2)M点的坐标为(0,4)或(0,﹣4);(3)①3<S△CDP+S△BOP<4;②∠DCP+∠BOP=∠CPO或∠DCP﹣∠BOP=∠CPO或∠DCP﹣∠BOP=∠CPO.
【解析】试题分析:(1)根据点的平移规律即可得点C,D的坐标;(2)由S平行四边形ABOC=ABCO即可计算出S平行四边形ABOC=8,设M坐标为(0,m),根据三角形面积公式得![]() ×4×|m|=8,解得m=±4,所以点M的坐标为(0,4)或(0,﹣4);(3)(3)①根据题意易得S梯形OCDB=7,当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;
×4×|m|=8,解得m=±4,所以点M的坐标为(0,4)或(0,﹣4);(3)(3)①根据题意易得S梯形OCDB=7,当点P运动到点B时,S△BOC的最小值=3,则可判断S△CDP+S△BOP<4,当点P运动到点D时,S△BOC的最大值=4,于是可判断S△CDP+S△BOP>3,所以3<S△CDP+S△BOP<4;
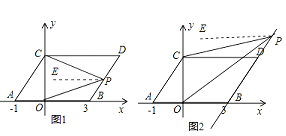
②分三种情况,第一种情况:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;第二种情况:当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO﹣∠EPC=∠BOP﹣∠DCP,于是∠BOP﹣∠DCP=∠CPO;第三种情况,当点P在线段DB的延长线上时,同第二种情况可得,当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.
试题解析:解:(1)由平移可知:C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S平行四边形ABOC=ABCO=4×2=8,
设M坐标为(0,m),
∴![]() ×4×|m|=8,解得m=±4
×4×|m|=8,解得m=±4
∴M点的坐标为(0,4)或(0,﹣4);
(3)①S梯形OCDB=![]() ×(3+4)×2=7,
×(3+4)×2=7,
当点P运动到点B时,S△BOC最小,S△BOC的最小值=![]() ×3×2=3,S△CDP+S△BOP<4,
×3×2=3,S△CDP+S△BOP<4,
当点P运动到点D时,S△BOC最大,S△BOC的最大值=![]() ×4×2=4,S△CDP+S△BOP>3,
×4×2=4,S△CDP+S△BOP>3,
所以3<S△CDP+S△BOP<4;
②当点P在BD上,如图1,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,作PE∥CD,
∵CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠EPO﹣∠EPC=∠BOP﹣∠DCP,
∴∠BOP﹣∠DCP=∠CPO;
同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 处于中间位置的数为这组数据的中位数
B. 中间两个数的平均数为这组数据的中位数
C. 要想了解一批电磁炉的使用寿命,适合采用全面调查的方法
D. 公司员工月收入的众数为3500元.说明该公司中月收入3500元的员工最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE∶OF等于( )
A. 2∶1 B. 3∶2 C. 2∶3 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在1.17-32-23中把省略的“+”号填上应得到( )
A. 1.17+32+23
B. -1.17+(-32)+(-23)
C. 1.17+(-32)+(-23)
D. 1.17-(+32)-(+23)
查看答案和解析>>
科目:初中数学 来源: 题型:
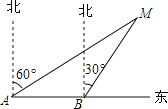
【题目】如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,AB=BC, BO是AC边上的中线,点P,D分别在AO和BC上,PB=PD,DE⊥AC于点E,


(1)求证:△BPO≌△PDE.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(先将图形补充完整,然后再证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com