
2011年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,丙绘制了不完整的两种统计图.

根据图中提供的信息,回答下列问题:
(1)参加演讲比赛的学生共有 人,并把条形图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形的圆心角为 度;
(3)学校欲从或A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求或A等级的小明参加市比赛的概率.
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作y轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xoy中,一次函数 的图象与x轴交于A(-1,0),与y轴交于点C.以直线x=2为对称轴的抛物线
的图象与x轴交于A(-1,0),与y轴交于点C.以直线x=2为对称轴的抛物线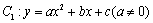 经过A、C两点,并与x轴正半轴交于点B.
经过A、C两点,并与x轴正半轴交于点B.
(1)(3分)求m的值及抛物线 的函数表达式.
的函数表达式.
(2)(5分)设点 ,若F是抛物线
,若F是抛物线 对称轴上使得△ADF的周长取得最小值的点,过F任意作一条与y轴不平行的直线交抛物线
对称轴上使得△ADF的周长取得最小值的点,过F任意作一条与y轴不平行的直线交抛物线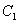 于
于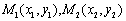 两点,试探究
两点,试探究 是否为定值?请说明理由.
是否为定值?请说明理由.
(3)(4分)将抛物线C1作适当平移,得到抛物线 ,若当
,若当 时,
时,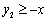 恒成立,求m的最大值.
恒成立,求m的最大值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com