
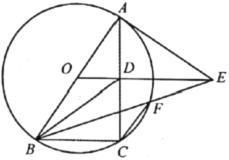
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是弦,点
是弦,点![]() 在圆外,
在圆外,![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 在第二象限,点
在第二象限,点![]() .
.
(1)如图①,求![]() 点坐标及
点坐标及![]() 的大小;
的大小;
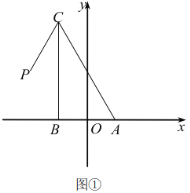
(2)将![]() 绕
绕![]() 点逆时针旋转得到
点逆时针旋转得到![]() ,点
,点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() 为
为![]() 的面积.
的面积.
①如图②,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
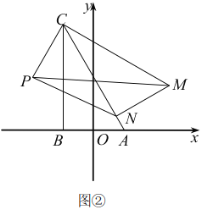
②求![]() 的取值范围(直接写出结果即可)
的取值范围(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
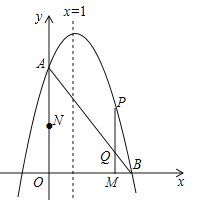
【题目】如图,已知抛物线![]() 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
(1)求此抛物线的解析式以及点B的坐标.
(2)动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
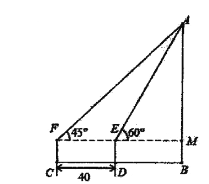
【题目】如图,为了测得某建筑物的高度![]() ,在
,在![]() 处用高为
处用高为![]() 米的测角仪
米的测角仪![]() ,测得该建筑物顶端
,测得该建筑物顶端![]() 的仰角为
的仰角为![]() ,再向建筑物方向前进
,再向建筑物方向前进![]() 米,又测得该建筑物顶端
米,又测得该建筑物顶端![]() 的仰角为
的仰角为![]() .
.
(1)填空:![]() ,
,![]() ;
;
(2)求该建筑物的高度![]() .(结果保留根号)
.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点A(m-2,n), B(m+4,n),C(m,
过点A(m-2,n), B(m+4,n),C(m,![]() ).
).
(1)b=__________(用含m的代数式表示);
(2)求△ABC的面积;
(3)当![]() 时,均有
时,均有![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
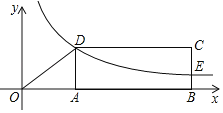
【题目】如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=
(k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=![]() ,则k的值_____.
,则k的值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把矩形沿EF折叠后,使点D恰好落 在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 图象与x轴交于点A,与y轴交于点B.
图象与x轴交于点A,与y轴交于点B.
(1)请直接写出点A坐标______,点B坐标________;
(2)点C是直线AB上一个动点,当△AOC的面积是△BOC的面积的2倍时,求点C的坐标;
(3)点D为直线AB上的一个动点,在平面内找另一个点E,且以O、B、D、E为顶点的四边形是菱形,请直接写出满足条件的菱形的周长_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com