
【题目】已知;如图,在△ABC中,AB=BC,∠ABC=90度.F为AB延长线上一点,点E在BC上,BE=BF,连接AE、EF和CF.

(1)求证:AE=CF;(2)若∠CAE=30°,求∠EFC的度数.
【答案】(1)见解析;(2)∠EFC=30°.
【解析】
(1)根据已知利用SAS判定△ABE≌△CBF,由全等三角形的对应边相等就可得到AE=CF;(2)根据已知利用角之间的关系可求得∠EFC的度数.
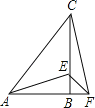
(1)证明:在△ABE和△CBF中,
∵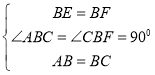 ,
,
∴△ABE≌△CBF(SAS).
∴AE=CF.
(2)解:∵AB=BC,∠ABC=90°,∠CAE=30°,
∴∠CAB=∠ACB=![]() (180°﹣90°)=45°,∠EAB=45°﹣30°=15°.
(180°﹣90°)=45°,∠EAB=45°﹣30°=15°.
∵△ABE≌△CBF,
∴∠EAB=∠FCB=15°.
∵BE=BF,∠EBF=90°,
∴∠BFE=∠FEB=45°.
∴∠EFC=180°﹣90°﹣15°﹣45°=30°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的夹角为α,则用[ρ,α]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[![]() ,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
A. (-2,2![]() ) B. (2,-2
) B. (2,-2![]() ) C. (-2
) C. (-2![]() ,-2) D. (-4,-4
,-2) D. (-4,-4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D,当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC此时BE与DC有怎样的位置关系?________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长为1,格点三角形![]() (顶点是网格线的交点的三角形)的顶点
(顶点是网格线的交点的三角形)的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
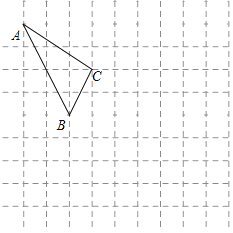
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)点![]() 到
到![]() 轴的距离是 ;
轴的距离是 ;
(3)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(4)写出点![]() 的坐标 .
的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
(1)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.(要求:填上适当的代数式,完成表格)
速度(千米/时) | 所用时间(时) | 所走的路程(千米) | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
(2)列出方程(组),并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
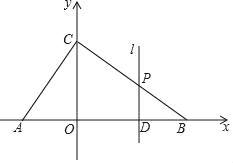
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠ACB=90°,OC、OB的长分别是一元二次方程x2﹣6x+8=0的两个根,且OC<OB.
(1)求点A的坐标;
(2)D是线段AB上的一个动点(点D不与点A,B重合),过点D的直线l与y轴平行,直线l交边AC或边BC于点P,设点D的横坐标为t,线段DP的长为d,求d关于t的函数解析式;
(3)在(2)的条件下,当d=![]() 时,请你直接写出点P的坐标.
时,请你直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com