
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H.且点C是![]() 的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
的中点,若扇形的半径为3.则图中阴影部分的面积等于______.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
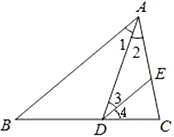
【题目】完成下面的推理填空
如图,已知![]() 是
是![]() 的角平分线,
的角平分线,![]() ,试证明:
,试证明:![]() .
.
证明:
![]() 是
是![]() 的角平分线(已知)
的角平分线(已知)
![]() ___________( )
___________( )
又![]() (已知)
(已知)
![]() ___________( )
___________( )
![]() ___________( )
___________( )
![]() ___________( )
___________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片的一角作折叠,使顶点 A 落在 A处, DE 为折痕,将 BEA对折,使得 B落在直线 EA上,得折痕 EG .
(1)求 DEG 的度数;
(2) 若 EA恰好平分 DEB ,求 DEA的度数 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小何按市场价格![]() 元/千克在收购了
元/千克在收购了![]() 千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
(![]() )若小何想将这批蘑菇存放
)若小何想将这批蘑菇存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
(![]() )小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为
)小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为![]() 元?
元?
(![]() )将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)此次共调查了 名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是 度;
(2)请把这个条形统计图补充完整;
(3)现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中的传播速度y(m/s)随气温x(℃)的变化而变化.下表给出了一组不同气温下声音传播的速度:
x(℃) | 0 | 5 | 10 | 15 | 20 | 25 |
y(m/s) | 331 | 334 | 337 | 340 | 343 | 346 |
(1)当x的值为35时,求对应的y的值;
(2)求y与x的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
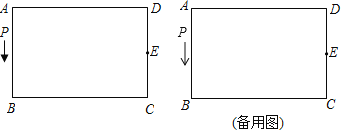
【题目】如图,已知长方形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 为长方形
为长方形![]() 边上的动点,动点
边上的动点,动点![]() 以
以![]() 个单位/秒的速度从
个单位/秒的速度从![]() 出发,沿着
出发,沿着![]() 运动到
运动到![]() 点停止,设点
点停止,设点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() 。
。
(1)求当![]() 时,
时,![]() 的值是________;当
的值是________;当![]() 时,
时,![]() 的值是________.
的值是________.
(2)当点![]() 在
在![]() 上时,求出
上时,求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)当![]() 在线段
在线段![]() 上运动到某一时刻时,
上运动到某一时刻时,![]() 的周长最小时,求此时
的周长最小时,求此时![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com