
【题目】综合题 ——
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.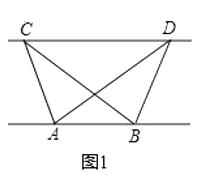
(2)结论应用:
①如图2,点M、N在反比例函数y= ![]() (k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;
(k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;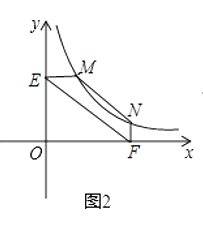
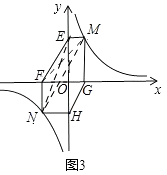
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.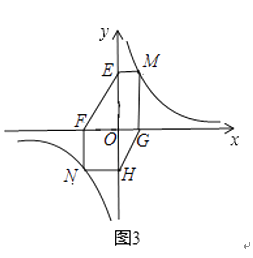
【答案】
(1)解:如图1,过点C作⊥AB于G,过点D作DH⊥AB于H,
∴∠CGA=∠DHB=90°,
∴CG∥DH,
∵△ABC和△ABD的面积相等,
∴CG=DH,
∴四边形CGHD是平行四边形、
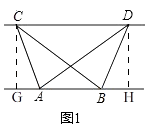
(2)解:①如图2,连接MF,NE,
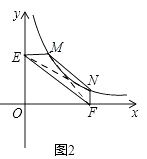
设M(x1,y1),N(x2,y2),
∵点M,N在反比例函数y= ![]() (k>0)的图象上,
(k>0)的图象上,
∴x1y1=k,x2y2=k,
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2,
∴S△EFM= ![]() x1x2=
x1x2= ![]() k,S△EFN=
k,S△EFN= ![]() x2y2=
x2y2= ![]() k,
k,
∴S△EFM=S△EFN,
由(1)中的结论可知,MN∥EF;
②MN∥EF,理由:如图3,由(1)中的结论可知,MN∥EF.
【解析】(1)过点C作⊥AB于G,过点D作DH⊥AB于H,根据△ABC和△ABD的面积相等,去证明CG∥DH,CG=DH即可证得结论。
(2)连接MF,NE,先证明S△EFM=S△EFN,然后利用(1)的结论得证。
【考点精析】掌握平行线之间的距离和三角形的面积是解答本题的根本,需要知道两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P在y轴上,当
,点P在y轴上,当![]() 的值最小时,P的坐标是
的值最小时,P的坐标是![]()
![]()
A. (0,1)B. (0,![]() )C. (0,0)D. (0,
)C. (0,0)D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
![]() 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且![]() ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求![]() 的度数;
的度数;
![]() 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点,![]() ,MN交
,MN交![]() 的外角平分线于点N,求
的外角平分线于点N,求![]() 的值;
的值;
![]() 如图3,过点A作
如图3,过点A作![]() 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边![]() ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=7,EF=3,则BC长为( )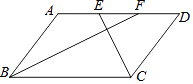
A.9
B.10
C.11
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
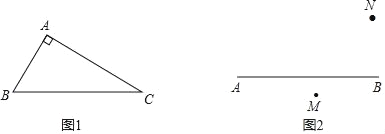
【题目】(1)如图1,在Rt△ABC中,AB=3,AC=4,BC=5,若直线EF垂直平分BC,请你利用尺规画出直线EF;
(2)若点P在(1)中BC的垂直平分线EF上,请直接写出PA+PB的最小值,回答PA+PB取最小值时点P的位置并在图中标出来;
解:PA+PB的最小值为 ,PA+PB取最小值时点P的位置是 ;
(3)如图2,点M,N分别在直线AB两侧,在直线AB上找一点Q,使得∠MQB=∠NQB.要求画图,并简要叙述确定点Q位置的步骤(无需尺规作图,保留画图痕迹,无需证明)
解:确定点Q位置的简要步骤: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com