练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线y=ax2+bx+c（a≠0）过点A（1，﹣3）、B（3，﹣3）、C（﹣1，5），顶点为M点．在抛物线上是找一点P使∠POM=90°，则P点的坐标_____．

    【答案】（，）

    【解析】

    根据题意，把抛物线经过的三点代入函数的表达式，列出方程组，解出各系数，再确抛物线的顶点M的坐标．可求出直线OM的解析式，由于直线OP与直线PM垂直，因此两直线的斜率的积为1，由此可求出直线OP的解析式；联立抛物线的解析式即可求出P点坐标．

    抛物线y＝ax2＋bx＋c（a≠0）过点A（1，3）、B（3，3）、C（1，5），

    所以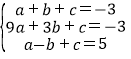，解得：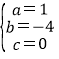

    所以抛物线的解析式为：y＝x24x＝（x2）24，顶点M坐标是（2，4），

    因此直线OM的解析式为y＝2x，

    由于直线PO与直线OM垂直，因此直线PO的解析式为y＝x，

    联立抛物线的解析式有：，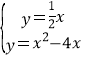

    解得，

    因此P点坐标为（，）．

    故答案为：（，）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

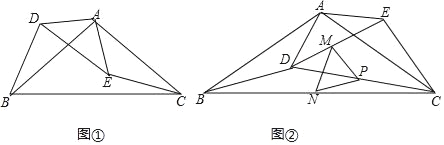
    【题目】如图①，在等腰△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE=120°．

    （1）求证：△ABD≌△ACE；

    （2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；

    （3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD=4，AB=6，请分别求出△PMN周长的最小值与最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O为△ABC的外接圆，BC为⊙O的直径，AE为⊙O的切线，过点B作BD⊥AE于D．

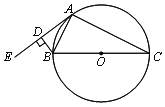
    （1）求证：∠DBA=∠ABC；

    （2）如果BD=1，tan∠BAD=，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】台州某校七（1）班同学分三组进行数学活动，对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据．

    根据以上信息，请回答下列问题：

    （1）七年级400名同学中最喜欢喝“冰红茶”的人数是多少？

    （2）补全八年级300名同学中零花钱的最主要用途情况频数分布直方图；

    （3）九年级300名同学中完成家庭作业的平均时间大约是多少小时（结果保留一位小数）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和40，则△EDF的面积为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察推理：如图1，△ABC中，∠ACB=90°，AC=BC，直线l过点C，点A、B在直线l同侧，BD⊥l，AE⊥l，垂足分别为D、E．

    （1）求证：△AEC≌△CDB；

    （2）类比探究：如图2，Rt△ABC中，∠ACB=90°，AC=6，将斜边AB绕点A逆时针旋转90°至AB′，连接B′C，求△AB′C的面积；

    （3）拓展提升：如图3，∠E=60°，EC=EB=4cm，点O在BC上，且OC=3cm，动点P从点E沿射线EC以2cm/s速度运动，连结OP，将线段OP绕点O逆时针旋转120°得到线段OF．要使点F恰好落在射线EB上，求点P运动的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，一次函数y=﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B．

    （1）线段AB，BC，AC的长分别为AB=　 　，BC=　 　，AC=　 　；

    （2）折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2．

    请从下列A、B两题中任选一题作答，我选择　 　题．

    A：①求线段AD的长；

    ②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由．

    B：①求线段DE的长；

    ②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．

    （1）求证：AB=CD；

    （2）若AB=CF，∠B=30°，求∠D的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，完成任务：

    自相似图形

    定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．

    任务：

    （1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为　 　；

    （2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为　 　；

    （3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．

    请从下列A、B两题中任选一条作答：我选择　 　题．

    A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=　 　（用含b的式子表示）；

    ②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=　 　（用含n，b的式子表示）；

    B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=　 　（用含b的式子表示）；

    ②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=　 　（用含m，n，b的式子表示）．

    查看答案和解析>>

    同步练习册答案