
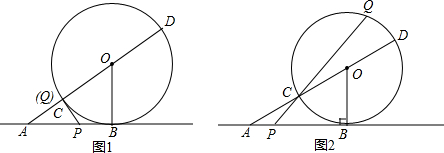
分析 (1)首先根据题意得到PC为⊙O的切线,在Rt△ACP中,利用锐角三角形函数值的定义求出AP的长;
(2)首先根据题意可得到△CQD中CD边上的高为1,进而作出图形得到答案;
(3)过点P作PM⊥AD于点M,过点Q作QN⊥AD于点N,连接QD,根据相似三角形的性质可得QN2=CN×DN,设CN=x,则DN=4-x,列出x的方程,求出x的值,进而求出AP的长度.
解答 解:(1)∵AB是⊙O的切线,
∴∠OBA=90°,
∵Rt△ABC中,直径CD=4,∠DAB=30°,
∴OB=OC=AC=2,
∵当点P运动到Q、C两点重合时,PC为⊙O的切线,
∴∠PCA=90°,
∵∠DAB=30°,AC=2,
∴AP=$\frac{4\sqrt{3}}{3}$,
(2)4种,如图1,由CD=4,S△CQD=2,
故CD上的高的长度为1,由图可知有4个位置使△CDQ的面积为2;
(3)过点P作PM⊥AD于点M,过点Q作QN⊥AD于点N,连接QD,
∵S△CQD=2,
∴$\frac{1}{2}$QN×CD=2,
∴QN=1,
∵CD是圆O的直径,
∴∠CQD=90°
易证△QCN∽△DQN,
∴$\frac{QN}{DN}=\frac{CN}{QN}$,
∴QN2=CN×DN,
设CN=x,则DN=4-x,
∴x(4-x)=1,
解得:x=2±$\sqrt{3}$,
∵CQ>QD,
∴CN=2+$\sqrt{3}$,
∴$\frac{CN}{QN}$=2+$\sqrt{3}$,
易证:△PMC∽△QNC,得:$\frac{CN}{QN}=\frac{CM}{MP}$=2+$\sqrt{3}$,
∴CM=2(2+$\sqrt{3}$)MP,
在Rt△AMP中易得:AM=$\sqrt{3}$MP,
∵AM+CM=AC=2,
∴(2+$\sqrt{3}$)MP+$\sqrt{3}$MP=2,
∴MP=$\frac{\sqrt{3}-1}{2}$,
∴AP=2MP=$\sqrt{3}$-1.
点评 本题主要考查了圆的综合题的知识,此题涉及到了相似三角形的判定与性质、切线的性质、平行线的性质以及勾股定理的知识,解答本题的关键是正确地作出辅助线利用相似三角形的性质解答,此题有一定的难度.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
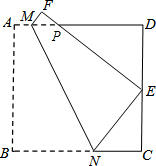 如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,EF交AD于点P.若△PDE的周长为18,且AM=2,求线段EC的长.
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,EF交AD于点P.若△PDE的周长为18,且AM=2,求线段EC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电信部门要在S区修建一座发射塔.按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.(尺规作图)
如图,电信部门要在S区修建一座发射塔.按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.(尺规作图)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com