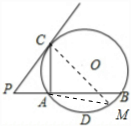
(1)证明:连接CO并延长交⊙O于M,连接AM,
∵PC
2=PA•PB,
∴
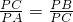
.
∵∠P=∠P,
∴△PAC∽△PCB,∠PCA=∠B.
∵∠B=∠M,
∴∠M=∠PCA.
∵CM是直径,
∴∠MAC=90°.
∴∠ACM+∠M=90°.
∴∠ACM+∠PCA=90°.
即∠PCM=90°.
∴CM⊥PC.
∴PC是⊙O的切线.
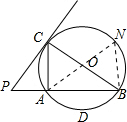
(2)解:连接AO,并延长AO交⊙O于N,连接BN,
∵AN是直径,
∴∠ABN=90°∠N=∠ACB,AN=12.
在Rt△ABN中,AB=ANsin∠ACB=12sin∠ACB=12×

=

.
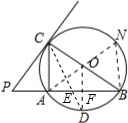
(3)解:连接OD交AB于F,
∴OD⊥AB.
∵D是劣弧AB的中点,
∴∠ACD=∠BCD.
∵∠PCA=∠B,
∴∠PCE=∠PEC.
∴PC=PE由△PCA∽△PBC得PC=3PA.
∵PC
2=PA•PB,
∴9PA
2=PA•PB.
∴9PA=PB=PA+AB.
∴8PA=AB=

.
∴PA=

.
∴PC=PE=
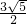
.
AE=

,AB=

,AF=

,EF=

在Rt△OAF中,可求得OF=4,
∴DF=OD-OF=6-4=2,
∴DE=3.
∵AE•EB=DE•CE,
∴CE=5.
分析:(1)连接CO并延长交⊙O于M,连接AM,根据两组对应边的比相等且相应的夹角相等的两个三角形相似得到△PAC∽△PCB,从而得到∠PCA=∠B,再根据角之间的关系可得到CM⊥PC即PC是⊙O的切线;
(2)连接AO,并延长AO交⊙O于N,连接BN,根据同弧所对角相等得到∠N=∠ACB,已知AN的长及sin∠ACB的值,根据三角函数公式即可求得AB的长;
(3)连接OD交AB于F,由已知可推出△PCA∽△PBC,根据对应边的相似比相等可求得PA,PC的长,再根据勾股定理求得OF的长,那么再求CE的长就不难了.
点评:此题主要考查学生对切线的判定,解直角三角形及相似三角形的判定等知识点的综合运用.

 如图,点P是半径为6的⊙O外一点,过点P作⊙O的割线PAB,点C是⊙O上一点,且PC2=PA•PB.求证:
如图,点P是半径为6的⊙O外一点,过点P作⊙O的割线PAB,点C是⊙O上一点,且PC2=PA•PB.求证: ,求弦AB的长;
,求弦AB的长; (1)证明:连接CO并延长交⊙O于M,连接AM,
(1)证明:连接CO并延长交⊙O于M,连接AM,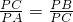 .
.
 =
= .
.
 .
. .
.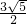 .
. ,AB=
,AB= ,AF=
,AF= ,EF=
,EF=


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.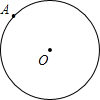 如图,点A是半径为
如图,点A是半径为