
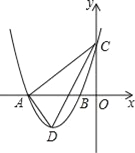
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=ax2+bx+3ÓėxÖį½»ÓŚA£Ø©4£¬0£©”¢B£Ø©l£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£¬µćDŹĒµŚČżĻóĻŽµÄÅ×ĪļĻßÉĻŅ»¶Æµć£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ÉčµćDµÄŗį×ų±źĪŖm£¬”÷ACDµÄĆ껿ĪŖĮæĒó³öSÓėmµÄŗÆŹż¹ŲĻµŹ½£¬²¢Č·¶ØmĪŖŗĪÖµŹ±SÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ¶ąÉŁ£æ
£Ø3£©ČōµćPŹĒÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»µć£¬ŹĒ·ń“ęŌŚµćPŹ¹µĆ”ĻAPC=90”ć£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y=![]() x2+
x2+![]() x+3£»£Ø2£©mĪŖ©2Ź±SÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ6£Ø3£©PµÄ×ų±źĪŖ£Ø©
x+3£»£Ø2£©mĪŖ©2Ź±SÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ6£Ø3£©PµÄ×ų±źĪŖ£Ø©![]() £¬
£¬ ![]() £©»ņ£Ø©
£©»ņ£Ø©![]() £¬
£¬ ![]() £©
£©
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ(1)”¢½«µćAŗĶµćBµÄ×ų±ź“śČė½āĪöŹ½£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öŗÆŹż½āĪöŹ½£»(2)”¢Ź×ĻČĒó³öµćCµÄ×ų±ź£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·ØĒó³öÖ±ĻßACµÄŗÆŹż½āĪöŹ½£¬¹żµćD D×÷DE”ĪyÖį£¬½»ACÓŚµćE£¬Éč³öµćDŗĶµćEµÄ×ų±ź£¬Č»ŗóĒó³öDEµÄ³¤¶Č£¬øł¾ŻĆ껿µÄ¼ĘĖć¹«Ź½µĆ³öĆ껿µÄ¶ž“ĪŗÆŹż½āĪöŹ½£¬“Ó¶ųµĆ³öĆ껿µÄ×ī“óÖµ£»(3)”¢ŅŌACĪŖÖ±¾¶×÷Ō²½»Å×ĪļĻߵĶŌ³ĘÖįÓŚP£¬øł¾ŻµćA ŗĶµćCµÄ×ų±źµĆ³öÖŠµćµÄ×ų±ź£¬Ēó³öACŗĶOPµÄ³¤¶Č£¬ÉčµćPµÄ×ų±źĪŖ£Ø![]() £¬y£©£¬Č»ŗóøł¾Ż¹“¹É¶ØĄķĒó³öyµÄÖµ£¬µĆ³öµćPµÄ×ų±ź£®
£¬y£©£¬Č»ŗóøł¾Ż¹“¹É¶ØĄķĒó³öyµÄÖµ£¬µĆ³öµćPµÄ×ų±ź£®
ŹŌĢā½āĪö£ŗ(1)”¢½«A£Ø©4£¬0£©”¢B£Ø©l£¬0£©“śČėy=ax2+bx+3µĆ£ŗ![]() £¬
£¬
½āµĆ![]() £¬ ¹ŹÅ×ĪļĻßµÄŗÆŹż½āĪöŹ½ĪŖy=
£¬ ¹ŹÅ×ĪļĻßµÄŗÆŹż½āĪöŹ½ĪŖy=![]() x2+
x2+![]() x+3£»
x+3£»
(2)”¢Įīx=0£¬Ōņy=3£¬ ”ąC£Ø0£¬3£©£¬
ÉčÖ±ĻßACµÄ½āĪöŹ½ĪŖy=mx+n£¬ “śČėA£Ø©4£¬0£©”¢C£Ø0£¬3£©µĆ![]() £¬ ½āµĆ
£¬ ½āµĆ![]()
”ąACµÄ½āĪöŹ½ĪŖy=![]() x+3£»
x+3£»
¹żD×÷DE”ĪyÖį£¬½»ACÓŚµćE£¬ÉčD£Øm£¬![]() m2+
m2+![]() m+3£©£¬E£Øm£¬
m+3£©£¬E£Øm£¬![]() m+3£©£Ø©4£¼m£¼©1£©£¬ ŌņDE=
m+3£©£Ø©4£¼m£¼©1£©£¬ ŌņDE=![]() m+3©£Ø
m+3©£Ø![]() m2+
m2+![]() m+3£©£¬ ”ąDE=©
m+3£©£¬ ”ąDE=©![]() m2©3m£¬
m2©3m£¬
”ąS=![]() DE”Į4=2£Ø©
DE”Į4=2£Ø©![]() m2©3m£©=©
m2©3m£©=©![]() m2©6m=©
m2©6m=©![]() £Øm+2£©2+6£¬
£Øm+2£©2+6£¬
”ąm=©2Ź±£¬S×ī“ó=6£» ¹ŹmĪŖ©2Ź±SÓŠ×ī“óÖµ£¬×ī“óÖµŹĒ6£®
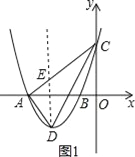
(3)”¢“ęŌŚµćPŹ¹µĆ”ĻAPC=90”ć£¬ ŅŌACĪŖÖ±¾¶×÷Ō²½»Å×ĪļĻߵĶŌ³ĘÖįÓŚP£¬
”ßA£Ø©4£¬0£©”¢C£Ø0£¬3£©£¬ ”ąACµÄÖŠµćOµÄ×ų±źĪŖ£Ø©2£¬![]() £©£¬AC=
£©£¬AC=![]() =5£¬
=5£¬
”ąOP=![]() =
=![]() £¬ ”ßÅ×ĪļĻßy=ax2+bx+3ÓėxÖį½»ÓŚA£Ø©4£¬0£©”¢B£Ø©l£¬0£©Į½µć£¬
£¬ ”ßÅ×ĪļĻßy=ax2+bx+3ÓėxÖį½»ÓŚA£Ø©4£¬0£©”¢B£Ø©l£¬0£©Į½µć£¬
”ą¶Ō³ĘÖįx=![]() =©
=©![]() £¬ ÉčP£Ø©
£¬ ÉčP£Ø©![]() £¬y£©£¬ ”ąOP2=£Ø
£¬y£©£¬ ”ąOP2=£Ø![]() £©2£¬
£©2£¬
¼“£Ø©2+![]() £©2+£Ø
£©2+£Ø![]() ©y£©2=£Ø
©y£©2=£Ø![]() £©2£¬ ½āµĆy=
£©2£¬ ½āµĆy=![]() ”Ą
”Ą![]() £¬
£¬
”ąPµÄ×ų±źĪŖ£Ø©![]() £¬
£¬![]() £©»ņ£Ø©
£©»ņ£Ø©![]() £¬
£¬![]() £©£®
£©£®


 ŹĄ¼Ķ°ŁĶØĘŚÄ©½š¾ķĻµĮŠ“š°ø
ŹĄ¼Ķ°ŁĶØĘŚÄ©½š¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
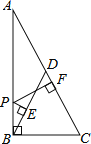
”¾ĢāÄæ”æČēĶ¼£®ŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬µćDŹĒŠ±±ßÉĻµÄÖŠµć£¬µćPŌŚABÉĻ£¬PE”ĶBDÓŚE£¬PF”ĶACÓŚF£¬ČōAB=6£¬BC=3£¬ŌņPE+PF=£Ø””””£©
A. ![]()
B. ![]()
C. ![]()
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() £Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬ÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©1£¬0£©£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
£Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬ÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©1£¬0£©£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
¢Ł4ac£¼b2£»
¢Ś·½³Ģ![]() µÄĮ½øöøłŹĒx1=©1£¬x2=3£»
µÄĮ½øöøłŹĒx1=©1£¬x2=3£»
¢Ū3a+c£¾0
¢Üµ±y£¾0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ©1”Üx£¼3
¢Żµ±x£¼0Ź±£¬yĖęxŌö“ó¶ųŌö“ó
ĘäÖŠ½įĀŪÕżČ·µÄøöŹżŹĒ£Ø””””£©

A. 4øö B. 3øö C. 2øö D. 1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOÖ±¾¶£¬CDĪŖ”ŃOµÄĒŠĻߣ¬CĪŖĒŠµć£¬¹żA×÷CDµÄ“¹Ļߣ¬“¹×ćĪŖD£®
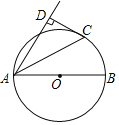
£Ø1£©ĒóÖ¤£ŗACĘ½·Ö”ĻBAD£»
£Ø2£©Čō”ŃO°ė¾¶ĪŖ5£¬CD£½4£¬ĒóADµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³Ė®Ę½µŲĆęÉĻ½ØÖžĪļµÄø߶ČĪŖAB£¬ŌŚµćDŗĶµćF“¦·Ö±šŹśĮ¢øߏĒ2Ć׵ıźøĖCDŗĶEF£¬Į½±źøĖĻąøō52Ć×£¬²¢ĒŅ½ØÖžĪļAB£¬±źøĖCDŗĶEFŌŚĶ¬Ņ»ŹśÖ±Ę½ĆęÄŚ£¬“Ó±źøĖCDŗóĶĖ2Ć×µ½µćG“¦£¬ŌŚG“¦²āµĆ½ØÖžĪļ¶„¶ĖAŗĶ±źøĖ¶„¶ĖCŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£»“Ó±źøĖFEŗóĶĖ4Ć×µ½µćH“¦£¬ŌŚH“¦²āµĆ½ØÖžĪļ¶„¶ĖAŗĶ±źøĖ¶„¶ĖEŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬Ēó½ØÖžĪļµÄøߣ®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
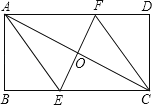
”¾ĢāÄæ”潫¾ŲŠĪABCDÕŪµžŹ¹A£¬CÖŲŗĻ£¬ÕŪŗŪ½»BCÓŚE£¬½»ADÓŚF£¬
£Ø1£©ĒóÖ¤£ŗĖıߊĪAECFĪŖĮāŠĪ£»
£Ø2£©ČōAB£½4£¬BC£½8£¬
¢ŁĒóĮāŠĪµÄ±ß³¤£»
¢ŚĒóÕŪŗŪEFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ōÖ½ŹĒÖŠ¹ś“«Ķ³µÄĆń¼äŅÕŹõ£¬Ėü»Ćę¾«ĆĄ£¬·ēøń¶ĄĢŲ£¬ÉīŹÜ“ó¼ŅĻ²°®£¬ĻÖÓŠČżÕŲ»ĶøĆ÷µÄæØʬ£¬ĘäÖŠĮ½ÕÅæØʬµÄÕżĆęĶ¼°øĪŖ”°½šÓć”±£¬ĮķĶāŅ»ÕÅæØʬµÄÕżĆęĶ¼°øĪŖ”°ŗūµū”±£¬æØʬ³żÕżĆę¼ōÖ½Ķ¼°ø²»Ķ¬Ķā£¬ĘäÓą¾łĻąĶ¬£®½«ÕāČżÕÅæØʬ±³ĆęĻņÉĻĻ“ŌČ“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£¬¼ĒĀ¼Ķ¼°øŗó·Å»Ų£¬ÖŲŠĀĻ“ŌČŗóŌŁ“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£®ĒėÓĆ»Ź÷דĶ¼£Ø»ņĮŠ±ķ£©µÄ·½·Ø£¬Ēó³é³öµÄĮ½ÕÅæØʬÉĻµÄĶ¼°ø¶¼ŹĒ”°½šÓć”±µÄøÅĀŹ£®£ØĶ¼°øĪŖ”°½šÓć”±µÄĮ½ÕÅæØʬ·Ö±š¼ĒĪŖA1”¢A2£¬Ķ¼°øĪŖ”°ŗūµū”±µÄæØʬ¼ĒĪŖB£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
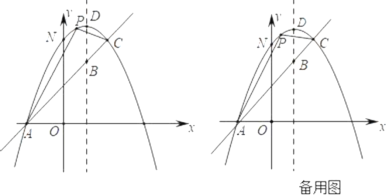
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½©x2+bx+cÓėŅ»Ö±ĻßĻą½»ÓŚA£Ø©1£¬0£©£¬C£Ø2£¬3£©Į½µć£¬ÓėyÖį½»ÓŚµćN£¬Ę䶄µćĪŖD£®
£Ø1£©ĒóÅ×ĪļĻß¼°Ö±ĻßACµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ČōPŹĒÅ×ĪļĻßÉĻĪ»ÓŚÖ±ĻßACÉĻ·½µÄŅ»øö¶Æµć£¬ÉčµćPµÄŗį×ų±źĪŖt£»
¢Łµ±S”÷ACP£½S”÷ACNŹ±£¬ĒóµćPµÄ×ų±ź£»
¢ŚŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”÷ACPŹĒŅŌACĪŖŠ±±ßµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒóµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ČōÅ×ĪļĻߵĶŌ³ĘÖįÓėÖ±ĻßACĻą½»ÓŚµćB£¬EĪŖÖ±ĻßACÉĻµÄČĪŅāŅ»µć£¬¹żµćE×÷EF”ĪBD½»Å×ĪļĻßÓŚµćF£¬ŅŌB£¬D£¬E£¬FĪŖ¶„µćµÄĖıߊĪÄÜ·ńĪŖĘ½ŠŠĖıߊĪ£æČōÄÜ£¬ĒėÖ±½ÓŠ“³öµćEµÄ×ų±ź£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy1=a£Øx+2£©2-3Óėy2=![]() £Øx-3£©2+1½»ÓŚµćA£Ø1£¬3£©£¬¹żµćA×÷xÖįµÄĘ½ŠŠĻߣ¬·Ö±š½»Į½ĢõÅ×ĪļĻßÓŚµćB£¬C£®ŌņŅŌĻĀ½įĀŪ£ŗ¢ŁĪŽĀŪxČ”ŗĪÖµ£¬y2µÄÖµ×ÜŹĒÕżŹż£»¢Śa=1£»¢Ūµ±x=0Ź±£¬y2-y1=4£»¢Ü2AB=3AC£»ĘäÖŠÕżČ·½įĀŪŹĒ£Ø””””£©
£Øx-3£©2+1½»ÓŚµćA£Ø1£¬3£©£¬¹żµćA×÷xÖįµÄĘ½ŠŠĻߣ¬·Ö±š½»Į½ĢõÅ×ĪļĻßÓŚµćB£¬C£®ŌņŅŌĻĀ½įĀŪ£ŗ¢ŁĪŽĀŪxČ”ŗĪÖµ£¬y2µÄÖµ×ÜŹĒÕżŹż£»¢Śa=1£»¢Ūµ±x=0Ź±£¬y2-y1=4£»¢Ü2AB=3AC£»ĘäÖŠÕżČ·½įĀŪŹĒ£Ø””””£©
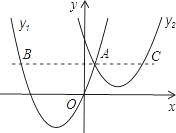
A.¢Ł¢ŚB.¢Ś¢ŪC.¢Ū¢ÜD.¢Ł¢Ü
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com