
【题目】甲口袋中放有3个红球和5个白球,乙口袋中放有7个红球和9个白球,所有球除颜色外都相同.充分搅匀两个口袋,分别从两个口袋中任意摸出一个球,设从甲中摸出红球的概率是![]() (红),从乙中摸出红球的概率是
(红),从乙中摸出红球的概率是![]() (红).
(红).
(1)求![]() (红)与
(红)与![]() (红)的值,并比较它们的大小.
(红)的值,并比较它们的大小.
(2)将甲、乙两个口袋的球都倒入丙口袋,充分搅匀后,设从丙中任意摸出一球是红球的概率为![]() (红).小明认为:
(红).小明认为:![]() (红)
(红)![]()
![]() (红)
(红)![]()
![]() (红).他的想法正确吗?请说明理由.
(红).他的想法正确吗?请说明理由.
【答案】(1) ![]() (红)
(红)![]() ,
,![]() (红)
(红)![]() ,
,![]() (红)<
(红)<![]() (红);(2)他的想法不正确,理由见解析.
(红);(2)他的想法不正确,理由见解析.
【解析】
(1)根据甲、乙两袋中红球的个数以及每个袋中球的总个数求出![]() (红)与
(红)与![]() (红),然后进行比较即可;
(红),然后进行比较即可;
(2)根据丙袋中红球的个数以及球的总个数求出![]() (红),与
(红),与![]() (红)
(红)![]()
![]() (红)进行比较即可.
(红)进行比较即可.
(1)甲袋中有球共3+5=8个,其中有红球3个,所以![]() (红)
(红)![]() ,
,
乙袋中有球共7+9=16个,其中有红球7个,所以![]() (红)
(红)![]() ,
,
因为![]() <
<![]() ,所以
,所以![]() ;
;
(2)他的想法不正确,理由如下:
将甲、乙两个口袋的球都倒入丙口袋,则丙袋中有球共3+5+7+9=24个,其中红球有3+7=10个,
所以从丙中任意摸出一球是红球的概率为![]() (红)=
(红)=![]() ,
,
而![]() (红)
(红)![]()
![]() (红)=
(红)= ![]() +
+![]() =
=![]() ,
,
![]() ,
,
所以小明的说法不正确.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C. ![]() <MN<
<MN<![]() D.
D. ![]() <MN≤
<MN≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
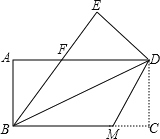
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,在图中画出分割线,拼出如图
,在图中画出分割线,拼出如图![]() 所示的新正方形.
所示的新正方形.

请你参考.上述做法,解决如下问题:
(1)现有![]() 个边长为
个边长为![]() 的正方形,排列形式如图
的正方形,排列形式如图![]() ,请把它们分割后拼接成一个新的正方形,在图
,请把它们分割后拼接成一个新的正方形,在图![]() 中画出分割线,并在图
中画出分割线,并在图![]() 的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为
的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为![]() )
)
(2)如图![]() ,现有由
,现有由![]() 个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.
个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
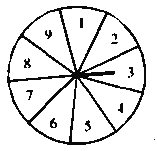
【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com