
 如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长.
如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长. 分析 分类画出图形,然后利用翻折的性质找出相等的边长,最后将三角形的三边转化为三角形ABC的两边的和进行求解即可.
解答 解:如图1所示:
由翻折的性质可知:AN=CN.
所以△CBN的周长=BC+NB+CN=CB+BN+AN=CB+AB=8+10=18.
如图2所示:
由翻折的性质可知:NC=BN.
△ANC的周长=AC+AN+CN=AC+AN+BN=AC+AB=6+10=16.
如图3所示
由翻折的性质可知:AM=BM.
△ACM的周长=AC+CM+AM=AC+CM+BM=AC+CB=6+8=14.
综上所述,没有重合部分所成的三角形的周长为18或16或14.
点评 本题主要考查的是翻折的性质,掌握翻折的性质,将三角形的周长转化为原三角形的两边之和是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
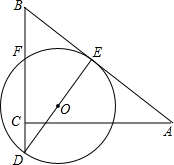 如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.
如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
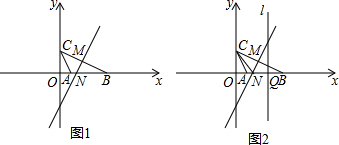
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
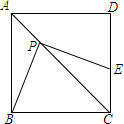 边长为1的正方形ABCD中,点P是对角线AC上一动点(不与点A、C重合),作PE⊥PB交CD于点E.
边长为1的正方形ABCD中,点P是对角线AC上一动点(不与点A、C重合),作PE⊥PB交CD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.
如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无解 | B. | 解为x=-3 | C. | 解为任意数 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com