
【题目】如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
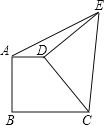
A. 1 B. 2 C. 3 D. 不能确定
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
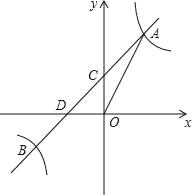
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)对于反比例函数y=![]() ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;
(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.若∠A'CA=18°,则∠A=____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是C的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
(1)求证:点O在AB的垂直平分线上;
(2)若∠CAD=20°,求∠BOF的度数.
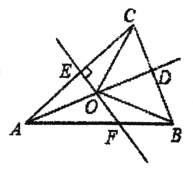
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
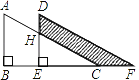
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB是边长为2+![]() 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=﹣![]() x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线 AB,CD 相交于点 O,且OE CD ,如图.
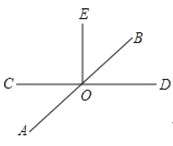
(1)过点 O 作直线 MN AB;
(2)若点 F 是(1)中所画直线 MN 上任意一点(O 点除外),且AOC 35°,求EOF的度数;
(3)若BOD:DOA 1:5,求AOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
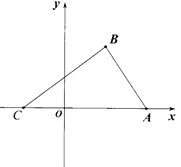
【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=![]() S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com