
【题目】关于一次函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.它的图象过点![]() B.它的图象经过第一、二、三象限
B.它的图象经过第一、二、三象限
C.![]() 随
随![]() 的增大而增大D.当
的增大而增大D.当![]() 时,总有
时,总有![]()
【答案】D
【解析】
A、利用一次函数图象上点的坐标特征可得出点(1,-2)不在一次函数y=1-2x的图象上,A不符合题意;
B、由k,b的值,利用一次函数图象与系数的关系可得出一次函数y=1-2x的图象经过第一、二、四象限,B不符合题意;
C、由k=-2<0,利用一次函数的性质可得出y随x的增大而减小,C不符合题意;
D、利用一次函数图象上点的坐标特征以及一次函数的性质,可得出当x>0时,总有y<1,D符合题意.
此题得解.
解:![]() 、当
、当![]() 时,
时,![]() ,
,
![]() 点
点![]() 不在一次函数
不在一次函数![]() 的图象上,
的图象上,![]() 不符合题意;
不符合题意;
![]() 、
、![]() ,
,![]() ,
,
![]() 一次函数
一次函数![]() 的图象经过第一、二、四象限,
的图象经过第一、二、四象限,![]() 不符合题意;
不符合题意;
![]() 、
、![]() ,
,
![]() 随
随![]() 的增大而减小,
的增大而减小,![]() 不符合题意;
不符合题意;
![]() 、
、![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,总有
时,总有![]() ,
,![]() 符合题意.
符合题意.
故选:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法:
![]() “明天降雨的概率是
“明天降雨的概率是![]() ”表示明天有半天都在降雨;
”表示明天有半天都在降雨;
![]() 无理数是开方开不尽的数;
无理数是开方开不尽的数;
![]() 若
若![]() 为实数,则
为实数,则![]() 是不可能事件;
是不可能事件;
![]() 的平方根是
的平方根是![]() ,用式子表示是
,用式子表示是![]() ;
;
![]() 某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为学校新年联欢会购买奖品,在某文具用品店购买明信片,每一张明信片的价格是8元,在结算时发现,如果再多买5张,就可以享受到打九折的优惠,总价格反而减少8元,为了能享受优惠,王老师比原计划多购买了5张明信片;
(1)王老师实际购买多少张明信片?一共花了多少钱?
(2)文具店开展元旦优惠活动:从即日起,在一周内,凭购物小票,累计购物超过500元,超过部分可以享受八折的优惠.王老师想了一想,又为学校购买了一定数量的笔记本,享受了八折优惠,这样,两次一共节省了36元,王老师购买笔记本实际花了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y1 与 y2 相交于点C , y1 与 x 轴交于点 D ,与 y 轴交于点0,1, y2 与 x 轴 交于点 B3,0,与 y 轴交于点 A ,下列说法正确的个数有( )
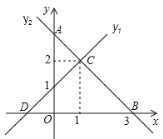
①y1的 解 析 式 为![]() ;② OA OB ;③
;② OA OB ;③![]() ;④
;④![]() ;⑤ AOB BCD .
;⑤ AOB BCD .
A.2 个B.3个C.4 个D.5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
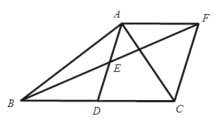
【题目】如图,在ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: AEF DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.

A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中数学 来源: 题型:
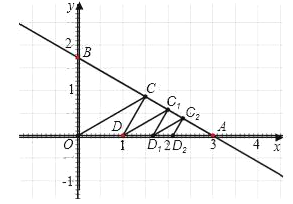
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
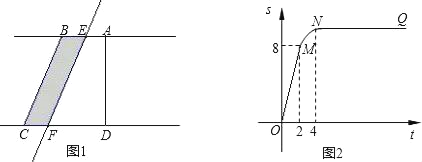
信息读取
(1)梯形上底的长AB= ;
(2)直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com