Question

【题目】已知，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF．求证：四边形ABCD是平行四边形．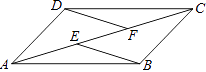

Answer 1

【答案】证明：∵DF∥BE ∴∠DFA=∠BEC
∵CF=AE，EF=EF
∴AF=CE
在△ADF和△CBE中，
∵
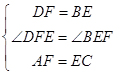
∴△ADF≌△CBE（SAS）
∴AD=BC
∴∠DAC=∠BCA
∴AD∥BC
∴四边形ABCD是平行四边形．

【解析】因为AE=CF，DF=BE，DF∥BE，所以可根据SAS判定△ADF≌△CBE，即有AD=BC，AD∥BC，故可根据一组对边平行且相等的四边形是平行四边形进行判定．
【考点精析】利用平行四边形的判定对题目进行判断即可得到答案，需要熟知两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．