
【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D , DE⊥AB , DF⊥AC , 垂足分别为E , F , AB=11,AC=5,则BE= . 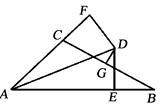
【答案】3
【解析】如图,连接CD,BD,
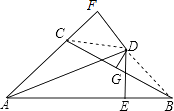
已知AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
根据角平分线的性质可得DF=DE,∠F=∠DEB=90°,∠ADF=∠A
即可得AE=AF,
又因DG是BC的垂直平分线,
所以CD=BD,
在Rt△CDF和Rt△BDE中,CD=BD,DF=DE,
利用HL定理可判定DF=DE,Rt△CDF ![]() Rt△BDE
Rt△BDE
由全等三角形的性质可得BE=CF,
所以AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
又因AB=11,AC=5,所以BE=3.
首先根据线段的垂直平分线的性质可连接CD、BD,有CD=BD,再根据角平分线的性质可得DF=DE,于是可证Rt△CDF ![]() Rt△BDE,由全等三角形的性质可得BE=CF,问题得解。
Rt△BDE,由全等三角形的性质可得BE=CF,问题得解。


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的开口向上,且经过点
的开口向上,且经过点![]() .
.
(1)若此抛物线经过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() .
.
①填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
②当![]() 的值最小时,求抛物线的解析式;
的值最小时,求抛物线的解析式;
(2)若![]() ,当
,当![]() ,抛物线上的点到
,抛物线上的点到![]() 轴距离的最大值为3时,求
轴距离的最大值为3时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
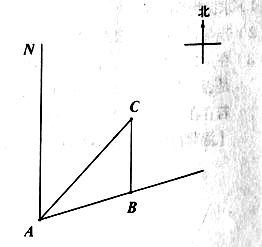
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点![]() 处测得码头
处测得码头![]() 的船的东北方向,航行40分钟后到达
的船的东北方向,航行40分钟后到达![]() 处,这时码头
处,这时码头![]() 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头
恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头![]() 的最近距离.(结果精确的0.1海里,参考数据
的最近距离.(结果精确的0.1海里,参考数据![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有一块长方形活动场地,长为 ![]() 米,宽比长少
米,宽比长少 ![]() 米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加
米,实施“阳光体育”行动以后,学校为了扩大学生的活动场地,让学生能更好地进行体育活动,将操场的长和宽都增加 ![]() 米.
米.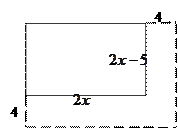
(1)求活动场地原来的面积是多少平方米.(用含 ![]() 的代数式表示)
的代数式表示)
(2)若 ![]() ,求活动场地面积增加后比原来多多少平方米.
,求活动场地面积增加后比原来多多少平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们实践活动中调查了20户家庭某月用电量,如表所示:
用电量(度) | 120 | 140 | 160 | 180 | 220 |
户数 | 2 | 4 | 5 | 7 | 2 |
则这户家庭用电量的众数和中位数分别是( )
A.180,160
B.160,180
C.160,160
D.180,180
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com