
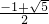 ,x2=
,x2=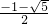


科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
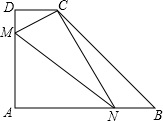 (2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.
(2013•同安区一模)如图所示,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,tanB=1.动点M、N分别从点D、B同时出发,沿线段DA和BA向A方向运动,动点N的运动速度是动点M运动速度的两倍,当点M或点N谁先运动到点A时,M、N两点同时停止运动.设动点M的运动速度是1个单位/秒,M、N运动的时间为x秒.查看答案和解析>>
科目:初中数学 来源:2012届浙江省衢州华茂外国语学校九年级上学期期末检测数学试卷(带解析) 题型:解答题
阅读材料,解答问题.
例 如图,在△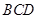 中,∠
中,∠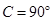 ,∠
,∠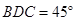 ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出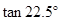 的值吗?
的值吗?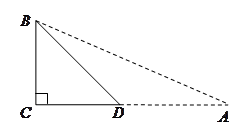
解:延长 到点
到点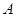 ,使
,使 ,连结
,连结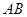 .
.
设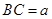 (
(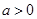 ).
).
∵在△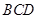 中,∠
中,∠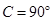 ,∠
,∠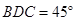 .
.
∴∠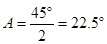 .
.
∴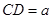 ,
,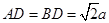 .
.
∴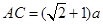 .
.
∴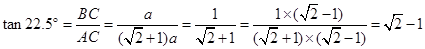 .
.
(1)仿照上例,求出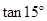 的值;
的值;
(2)在一次课外活动中,小刘从上例得到启发,用硬纸片做了两个直角三角形,如图1、图2.图1中,∠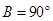 ,∠
,∠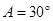 ,
,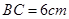 ;图2中,∠
;图2中,∠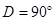 ,∠
,∠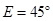 ,
,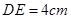 .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△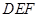 的直角边
的直角边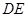 与△
与△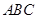 的斜边
的斜边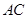 重合在一起,并将△
重合在一起,并将△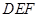 沿
沿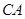 方向移动.在移动过程中,
方向移动.在移动过程中,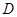 、
、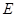 两点始终在
两点始终在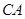 边上(移动开始时点
边上(移动开始时点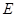 与点
与点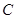 重合).
重合).
①在△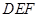 沿
沿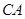 方向移动的过程中,∠
方向移动的过程中,∠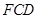 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)
②在△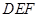 移动过程中,是否存在某个位置,使得∠
移动过程中,是否存在某个位置,使得∠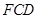
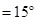 ?如果存在,求出
?如果存在,求出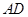 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.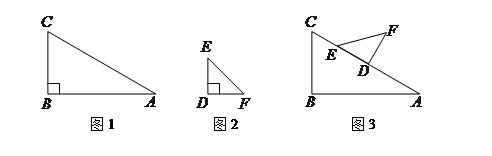
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省九年级上学期期末检测数学试卷(解析版) 题型:解答题
阅读材料,解答问题.
例 如图,在△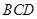 中,∠
中,∠ ,∠
,∠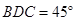 ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出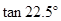 的值吗?
的值吗?

解:延长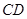 到点
到点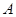 ,使
,使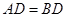 ,连结
,连结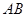 .
.
设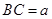 (
(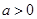 ).
).
∵在△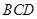 中,∠
中,∠ ,∠
,∠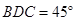 .
.
∴∠ .
.
∴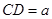 ,
,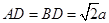 .
.
∴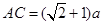 .
.
∴ .
.
(1)仿照上例,求出 的值;
的值;
(2)在一次课外活动中,小刘从上例得到启发,用硬纸片做了两个直角三角形,如图1、图2.图1中,∠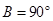 ,∠
,∠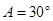 ,
,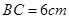 ;图2中,∠
;图2中,∠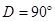 ,∠
,∠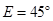 ,
,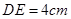 .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△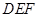 的直角边
的直角边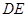 与△
与△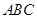 的斜边
的斜边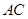 重合在一起,并将△
重合在一起,并将△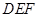 沿
沿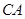 方向移动.在移动过程中,
方向移动.在移动过程中, 、
、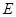 两点始终在
两点始终在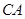 边上(移动开始时点
边上(移动开始时点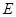 与点
与点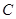 重合).
重合).
①在△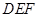 沿
沿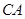 方向移动的过程中,∠
方向移动的过程中,∠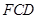 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)
②在△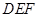 移动过程中,是否存在某个位置,使得∠
移动过程中,是否存在某个位置,使得∠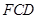
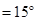 ?如果存在,求出
?如果存在,求出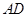 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
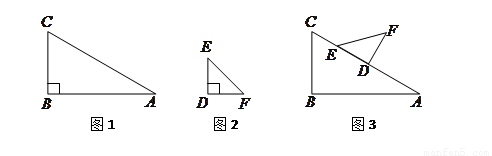
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com