
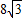 )两点的直线与直线
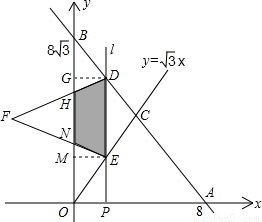
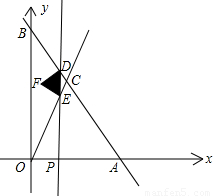
)两点的直线与直线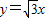 交于点C、平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线l的运动时间为t(秒).
交于点C、平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线l的运动时间为t(秒).
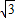 联立,得出的交点的坐标即为C点的坐标.而t的取值范围的最大值只要用C点横坐标除以1即可.
联立,得出的交点的坐标即为C点的坐标.而t的取值范围的最大值只要用C点横坐标除以1即可. 两条直线相交即可得出D、E关于t的坐标.再根据等边三角形各个角均为60°,做DE边上的高,运用勾股定理即可得出高的长度(关于t).再分别讨论t的取值,画出图形,代入各自对应的面积公式,化简后即可得出S关于t的方程.
两条直线相交即可得出D、E关于t的坐标.再根据等边三角形各个角均为60°,做DE边上的高,运用勾股定理即可得出高的长度(关于t).再分别讨论t的取值,画出图形,代入各自对应的面积公式,化简后即可得出S关于t的方程.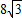 )分别代入解析式得,
)分别代入解析式得,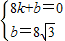 ,
,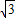 ,
,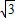 x+8
x+8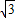 .
.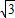 x+8
x+8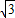 和y=
和y=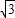 x组成方程组得,
x组成方程组得,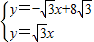 ,
,
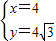 .
.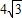 ),
),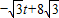 ),E的坐标是(t,
),E的坐标是(t,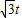 )
)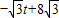 -
-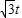 =
=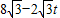 ;
;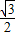 DE=12-3t;
DE=12-3t;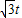 ),以及∠MNE=60°,
),以及∠MNE=60°,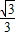 t,
t,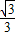 t,
t,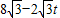 -
-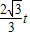 ,
,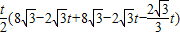
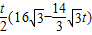
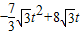 ;
;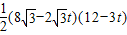
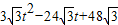 ;
;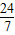 ,0);
,0);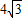 ,FP≥
,FP≥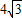 ,OP≤4,
,OP≤4,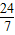 ,
, ,0).
,0).

科目:初中数学 来源:2010年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
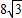 )两点的直线与直线
)两点的直线与直线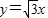 交于点C、平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线l的运动时间为t(秒).
交于点C、平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线l的运动时间为t(秒).
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《数据收集与处理》(06)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《图形的相似》(01)(解析版) 题型:选择题
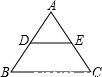
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《圆》(13)(解析版) 题型:解答题
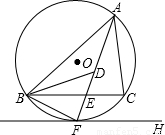
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com