
一个等腰三角形的面积为3m2,如图反映的是这个三角形的底边长a(m)和这边上的高h(m)之间关系的曲线图.

(1)根据图象填表;

(2)a的长能不能为0?
(3)当底取大于0的一个确定的值时,相应的高h确定吗?
(4)当底长为1.5m,12m时,你能求出相应的高吗?
(5)当高为2.5m,8m时,你能求出相应的底长吗?
(6)高h可以看成底a的函数吗?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| S△D1OC1+S△C1A1C2 |
| 2 |
| S△C1A1C2+S△C2A2C3 |
| 2 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
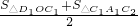 ,S右2=
,S右2=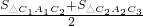 ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市拱墅区下城区中考数学一模试卷(解析版) 题型:解答题
 ,S右2=
,S右2= ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年江苏省无锡市江阴市初级中学中考数学模拟试卷(解析版) 题型:解答题
 ,S右2=
,S右2= ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级5月中考模拟数学试卷(解析版) 题型:解答题
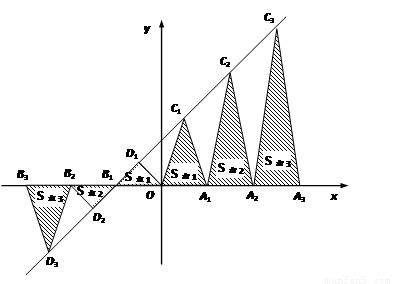
如图,以OA1=2为底边做等腰三角形,使得第三个顶点C1恰好在直线y=x+2上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线y=x+2上的等腰三角形.
(1)请你通过计算说明:底边为2,顶点在直线y=x+2上且面积为21的等腰三角形位于图
中什么位置?
(2)求证:y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半(如:S右1=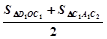 ,S右2=
,S右2=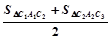 ).
).
(3)过D1、A1、C2三点画抛物线.问在抛物线上是否存在点P,使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com