
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
【答案】(Ⅰ)见解析;(Ⅱ)![]() ,
,![]() ;(Ⅲ)当
;(Ⅲ)当![]() 时,在甲林场一次购买树苗实际花费较少,见解析.
时,在甲林场一次购买树苗实际花费较少,见解析.
【解析】
(Ⅰ)根据甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折,进行计算即可
(Ⅱ)根据两林场不同的优惠方案以及实际花费=每棵树的单价![]() 树的棵数,列出分段函数
树的棵数,列出分段函数
(Ⅲ)根据两函数解析式分别讨论在哪个林场一次购买树苗,实际花费较少,求出对应的x的取值范围,即可得出结论
解:(I)
一次购买数(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | 400 | 720 |
在乙林场实际花费(元) | 200 | 285 | 370 | 710 |
(Ⅱ)根据愿意,得![]()
![]()
(Ⅲ)当![]() 时,有
时,有![]()
![]()
记![]() .由
.由![]() ,得
,得![]() .
.
由![]() ,有y随x的增大固增大,
,有y随x的增大固增大,
∴当![]() 时,
时,![]() .当
.当![]() 时,
时,![]() .
.
因此,当![]() 时,在甲林场一次购买树苗实际花费较少。
时,在甲林场一次购买树苗实际花费较少。
当![]() 时,在甲、乙两个林场一次购买树苗实际花费一样
时,在甲、乙两个林场一次购买树苗实际花费一样
当![]() 时,在乙林场一次购买树苗实际花费较少。
时,在乙林场一次购买树苗实际花费较少。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
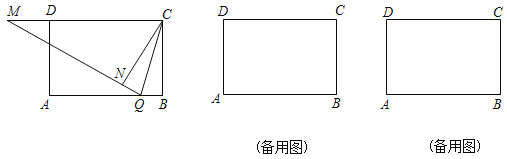
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
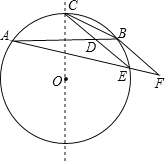
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令,某记者在一停车场对开车的司机进行了相关的调查,本次调查结果共有四种情况:①有时会喝点酒开车;②已戒酒或从不喝酒;③酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查情况整理并绘制成如下尚不完整的统计图,请根据相关信息,解答下列问题.
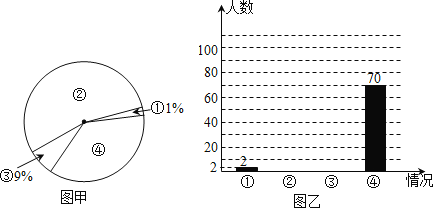
(1)该记者本次一共调查
了 名司机.
(2)求图①中④所在扇形的圆心角,并补全图②.
(3)在本次调查中,记者随机采访其中一名司机,求他属于第②种情况的概率.
(4)请估计在开车的10万名司机中,违反“酒驾”禁令的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,且关于直线
,且关于直线![]() 对称,
对称,![]() 是抛物线与x轴的一个交点.有下列结论:①方程
是抛物线与x轴的一个交点.有下列结论:①方程![]() 的一个根是x=-2;②若
的一个根是x=-2;②若![]() ,则
,则![]() ;③若
;③若![]() 时,方程
时,方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() ;④若
;④若![]() 时,
时,![]() ,则
,则![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
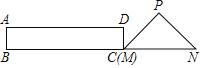
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A. 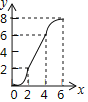 B.
B. 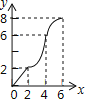 C.
C. 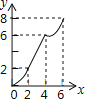 D.
D. 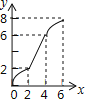
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十一届“汉语桥”世界中学生中文比赛复赛决赛在云南师范大学开赛.比赛吸引了来自99个国家110个赛区的332名师生来华.某校为了解全校学生对比赛中几类节目的喜爱情况(A:中国歌曲、B:中国民族舞蹈、C:中国曲艺、D:武术、E:其它表演),从全校学生中随机抽取部分学生进行问卷调查,要求每个学生选择一项最喜爱的节目,并把调查结果绘制成两幅不完整的统计图.

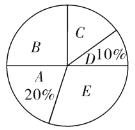
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;扇形统计图中,B节目所对应的圆心角是多少度;
(3)若该校有2400名学生,估计全校学生中喜欢中国民族舞蹈节目的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
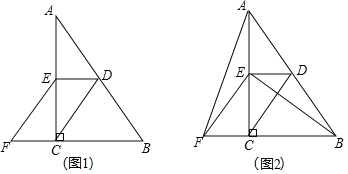
【题目】已知:如图,在![]() 中,
中,![]() ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且![]() .
.
![]() 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;
![]() 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与![]() 面积相等的三角形.
面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
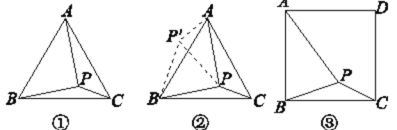
【题目】问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC的度数和等边三角形ABC的边长.
,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=![]() ,PB=
,PB=![]() ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com