
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A. 
(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
【答案】
(1)证明:∵∠BCD=90°,DE=EB,
∴EC=ED=EB,
∴∠EDC=∠ECD,
∵∠CED+∠CDE+∠DCE=180°,∠A+∠DCE+∠AFC=180°,
又∵∠CED=∠A,
∴∠CDE=∠AFC,
∴∠AFC=∠ACF,
∴AC=AF
(2)解:图象如图所示.
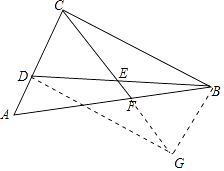
∵∠CED=∠ABG,∠CED=∠A,
∴∠A=∠ABG,
∴AC∥BG,
∴∠ECD=∠BGE,
在△CED和△GEB中,
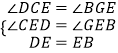 ,
,
∴△CED≌△GEB,
∴CE=EG,
∴CE=DE=EB,
∴CG=BD,CE=EG,DE=EB,
∴四边形CDGB是平行四边形,∵BD=CG,
∴四边形CDGB是矩形
【解析】(1)只要证明∠CDE=∠ECD,∠CDE=∠AFC即可解决问题.(2)只要证明CG=BD,CE=EG,DE=EB即可.
【考点精析】利用矩形的判定方法和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.
(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
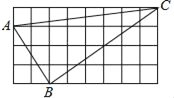
【题目】如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)判断△ABC是什么形状?并说明理由.
(2)求△ABC中BC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在 ![]() 的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
的中点,连接AF并延长与CB的延长线相交于点G,连接OF. 
(1)求证:OF= ![]() BG;
BG;
(2)若AB=4,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是多少千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式及定义域;
(3)甲车由A地前往B地比乙车由A地前往B地多用了多少小时.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com