
【题目】如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( ) 
A.∠ACB=90°
B.AC=2CD
C.∠DAB=65°
D.∠DAB+∠DCB=180°
【答案】B
【解析】解:A、∵AB是半圆的直径, ∴∠ACB=90°,故本选项正确;
B、∵点D是 ![]() 的中点,
的中点,
∴AD=CD,
∵AD+CD>AC,
∴AC<2CD,故本选项错误;
C、∵∠B=50°,
∴∠D=180°﹣∠B=130°,
∴∠DCA=∠DAC=25°,
∵∠ACB=90°,
∴∠BAC=40°,
∴∠BAD=∠BAC+∠DAC=65°,故本选项正确;
D、∠DAB+∠DCB=180°.正确.
故选B.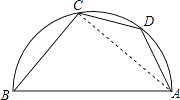
【考点精析】解答此题的关键在于理解圆心角、弧、弦的关系的相关知识,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y1=kx+b 与 y2=x+a 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当 x=3 时,y1=y2;④不等式 kx+b>x+a 的解集是 x<3,其中正确的结论有_______.(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(1,2).
(1)求m,n的值;
(2)请结合图象直接写出不等式mx+n>x+n-2的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个; B. 2个; C. 3个; D. 4个;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD、BF相交于点O,∠D=![]() ,下面判定两直线平行正确的是( )
,下面判定两直线平行正确的是( )

A. 当∠C=![]() 时,AB∥CD B. 当∠A=
时,AB∥CD B. 当∠A=![]() 时,AC∥DE
时,AC∥DE
C. 当∠E=![]() 时,CD∥EF D. 当∠BOC=
时,CD∥EF D. 当∠BOC=![]() 时,BF∥DE
时,BF∥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小红在某个路口统计20分钟各种车辆通过情况制成的统计表,其中空格处的字迹已模糊,但小红还记得7:50~8:00时段内的电瓶车车辆数与8:00~8:10时段内的货车车辆数之比是7∶2.
电瓶车 | 公交车 | 货车 | 小轿车 | 合计 | |
7:50~8:00 | 5 | 63 | 133 | ||
8:00~8:10 | 5 | 45 | 82 | ||
合计 | 67 | 30 | 108 |
(1)若在7:50~8:00时段,经过的小轿车数量正好是电瓶车数量的![]() ,求这个时段内的电瓶车通过的车辆数;
,求这个时段内的电瓶车通过的车辆数;
(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com