
如图1是由两块全等的含30°角的直角三角板摆放而成,斜边AC=10.
(1)若将△ADE沿直线AE翻折到如图2的位置,ED'与BC交于点F,求证:CF=EF;
(2)求EF的长;
(3)将图2中的△AD'E沿直线AE向右平移到图3的位置,使D'点落在BC上,求出平移的距离.
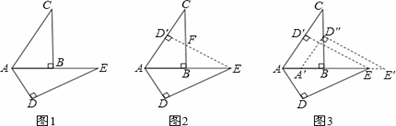
(1)证明:∵△ABC≌△ADE,
∴AC=AE,AB=AD,
根据翻折对称性,AD′=AD,
∴AD′=AB,
∴AC-AD′=AE-AB,
即CD′=BE,
在△CD′F与△EBF中,
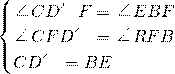
∴△CD′F≌△EBF(AAS), (4分)
∴CF=EF(全等三角形对应边相等);
(2)解:∵∠C=30°,AC=10,
∴AB=AC=×10=5,
∴EB=10-AB=5,
在△EFB中,∠FEB=30°,
∴BF=EF,
根据勾股定理得EF2=BF2+EB2,
∴EF2=(EF)2+52,
解得EF=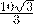 ; (4分)
; (4分)
(3)解:根据平移,D′D″∥AB,
又∵AD′=AB=5,CD′=10-AD′=5,
∴D′D″是△ABC的中位线,
∵∠C=30°,AC=10,
∴D′D″=AB=×AC=××10=,
故平移距离.


科目:初中数学 来源: 题型:
“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
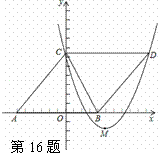
如图,在平面直角坐标系xoy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2﹣10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为 ;若点P在抛物线上且满足S△PBD=S△PCD,则点P的坐标为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
对于实数定义一种运算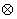 为:
为: ,有下列命题:
,有下列命题:
①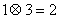 ;
;
②方程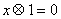 的根为:
的根为: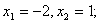
③不等式组 的解集为
的解集为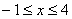
④在函数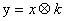 的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是
的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是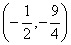 其中正确的( )
其中正确的( )
A.①②③④ B.①②③ C.①② D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
有四张卡片(形状、大小和质地都相同),正面分别写有字母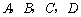 和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)
和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)
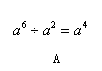
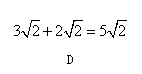
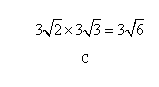
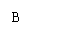
(1)用画树状图或列表法表示两次抽取卡片可能出现的所有情况(卡片可用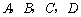 表示);
表示);
(2)分别求抽取的两张卡片上算式都正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处测得塔顶仰角∠ACB=30°
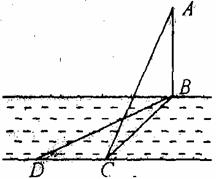 (1)若河宽BC是60米,求塔AB的高(精确到0.1米;参考数据)
(1)若河宽BC是60米,求塔AB的高(精确到0.1米;参考数据)
(2)若河宽BC无法度量.则应如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走a米到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高。(习题改编)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com